在上一章,我们学习了深度神经网络通常比浅层神经网络更加难以训练。我们有理由相信,若是可以训练深度网络,则能够获得比浅层网络更加强大的能力,但是现实很残酷。从上一章我们可以看到很多不利的消息,但是这些困难不能阻止我们使用深度神经网络。本章,我们将给出可以用来训练深度神经网络的技术,并在实战中应用它们。同样我们也会从更加广阔的视角来看神经网络,简要地回顾近期有关深度神经网络在图像识别、语音识别和其他应用中的研究进展。然后,还会给出一些关于未来神经网络又或人工智能的简短的推测性的看法。
这一章比较长。为了更好地让你们学习,我们先粗看一下整体安排。本章的小结之间关联并不太紧密,所以如果读者熟悉基本的神经网络的知识,那么可以任意跳到自己最感兴趣的部分。
本章主要的部分是对最为流行神经网络之一的深度卷积网络的介绍。我们将细致地分析一个使用卷积网络来解决 MNIST 数据集的手写数字识别的例子(包含了代码和讲解):
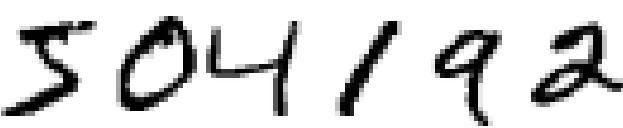
我们将从浅层的神经网络开始来解决上面的问题。通过多次的迭代,我们会构建越来越强大的网络。在这个过程中,也将要探究若干强大技术:卷积、pooling、使用GPU来更好地训练、训练数据的算法性扩展(避免过匹配)、dropout 技术的使用(同样为了防止过匹配现象)、网络的 ensemble 使用 和 其他技术。最终的结果能够接近人类的表现。在 10,000 幅 MNIST 测试图像上 —— 模型从未在训练中接触的图像 —— 该系统最终能够将其中 9,967 幅正确分类。这儿我们看看错分的 33 幅图像。注意正确分类是右上的标记;系统产生的分类在右下:

可以发现,这里面的图像对于正常人类来说都是非常困难区分的。例如,在第一行的第三幅图。我看的话,看起来更像是 “9” 而非 “8”,而 “8” 却是给出的真实的结果。我们的网络同样能够确定这个是 “9”。这种类型的“错误” 最起码是容易理解的,可能甚至值得我们赞许。最后用对最近使用深度(卷积)神经网络在图像识别上的研究进展作为关于图像识别的讨论的总结。
本章剩下的部分,我们将会从一个更加宽泛和宏观的角度来讨论深度学习。概述一些神经网络的其他模型,例如 RNN 和 LSTM 网络,以及这些网络如何在语音识别、自然语言处理和其他领域中应用的。最后会试着推测一下,神经网络和深度学习未来发展的方向,会从 intention-driven user interfaces 谈谈深度学习在人工智能的角色。 这章内容建立在本书前面章节的基础之上,使用了前面介绍的诸如 BP、规范化、softmax 函数,等等。然而,要想阅读这一章,倒是不需要太过细致地掌握前面章节中内容的所有的细节。当然读完第一章关于神经网络的基础是非常有帮助的。本章提到第二章到第五章的概念时,也会在文中给出链接供读者去查看这些必需的概念。
需要注意的一点是,本章所没有包含的那一部分。这一章并不是关于最新和最强大的神经网络库。我们也不是想训练数十层的神经网络来处理最前沿的问题。而是希望能够让读者理解深度神经网络背后核心的原理,并将这些原理用在一个 MNIST 问题的解决中,方便我们的理解。换句话说,本章目标不是将最前沿的神经网络展示给你看。包括前面的章节,我们都是聚焦在基础上,这样读者就能够做好充分的准备来掌握众多的不断涌现的深度学习领域最新工作。 本章仍然在Beta版。期望读者指出笔误,bug,小错和主要的误解。如果你发现了可疑的地方,请直接联系 mn@michaelnielsen.org。
卷积网络简介
在前面的章节中,我们教会了神经网络能够较好地识别手写数字:
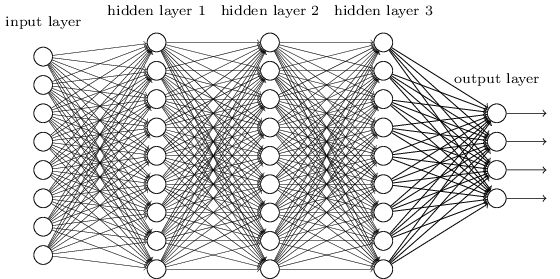
我们在深度神经网络中使用全连接的邻接关系。网络中的神经元与相邻的层上的所有神经元均连接:
特别地,对输入图像中的每个像素点,我们将其光强度作为对应输入层神经元的输入。对于 $$28 \times 28$$ 像素的图像,这意味着我们输入神经元需要有 $$784(=28 \times 28)$$ 个。
实践中的卷积神经网络
我们现已看到卷积神经网络中核心思想。现在我们就来看看如何在实践中使用卷积神经网络,通过实现某些卷积网络,应用在 MNIST 数字分类问题上。我们使用的程序是 network3.py,这是network.py 和 network2.py 的改进版本。代码可以在GitHub 下载。注意我们会在下一节详细研究一下代码。本节,我们直接使用 network3.py 来构建卷积网络。
network.py 和 network2.py 是使用 python 和矩阵库 numpy 实现的。这些程序从最初的理论开始,并实现了 BP、随机梯度下降等技术。我们既然已经知道原理,对 network3.py,我们现在就使用 Theano 来构建神经网络。使用 Theano 可以更方便地实现卷积网络的 BP,因为它会自动计算所有包含的映射。Theano 也会比我们之前的代码(容易看懂,运行蛮)运行得快得多,这会更适合训练更加复杂的神经网络。特别的一点,Theano 支持 CPU 和 GPU,我们写出来的 Theano 代码可以运行在 GPU 上。这会大幅度提升学习的速度,这样就算是很复杂的网络也是可以用在实际的场景中的。
如果你要继续跟下去,就需要安装 Theano。跟随这些参考 就可以安装 Theano 了。后面的例子在 Theano 0.6 上运行。有些是在 Mac OS X Yosemite上,没有 GPU。有些是在 Ubuntu 14.4 上,有 NVIDIA GPU。还有一些在两种情况都有运行。为了让 network3.py 运行,你需要在 network3.py 的源码中将 GPU 置为 True 或者 False。除此之外,让 Theano 在 GPU 上运行,你可能要参考 the instructions here。网络上还有很多的教程,用 Google 很容易找到。如果没有 GPU,也可以使用 Amazon Web Services EC2 G2 spot instances。注意即使是 GPU,训练也可能花费很多时间。很多实验花了数分钟或者数小时才完成。在 CPU 上,则可能需要好多天才能运行完最复杂的实验。正如在前面章节中提到的那样,我建议你搭建环境,然后阅读,偶尔回头再检查代码的输出。如果你使用 CPU,可能要降低训练的次数,甚至跳过这些实验。
为了获得一个基准,我们将启用一个浅层的架构,仅仅使用单一的隐藏层,包含 $$100$$ 个隐藏元。训练 $$60$$ 次,使用学习率为 $$\eta = 0.1$$,mini-batch 大小为 $$10$$,无规范化。Let‘s go:
>>> import network3
>>> from network3 import Network
>>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer
>>> training_data, validation_data, test_data = network3.load_data_shared()
>>> mini_batch_size = 10
>>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)卷积网络的代码
好了,现在来看看我们的卷积网络代码,network3.py。整体看来,程序结构类似于 network2.py,尽管细节有差异,因为我们使用了 Theano。首先我们来看 FullyConnectedLayer 类,这类似于我们之前讨论的那些神经网络层。下面是代码
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))__init__ 方法中的大部分都是可以自解释的,这里再给出一些解释。我们根据正态分布随机初始化了权重和偏差。代码中对应这个操作的一行看起来可能很吓人,但其实只在进行载入权重和偏差到 Theano 中所谓的共享变量中。这样可以确保这些变量可在 GPU 中进行处理。对此不做过深的解释。如果感兴趣,可以查看Theano documentation。而这种初始化的方式也是专门为 sigmoid 激活函数设计的(参见这里)。理想的情况是,我们初始化权重和偏差时会根据不同的激活函数(如 tanh 和 Rectified Linear Function)进行调整。这个在下面的问题中会进行讨论。初始方法 __init__ 以 self.params = [self.W, self.b] 结束。这样将该层所有需要学习的参数都归在一起。后面,Network.SGD 方法会使用 params 属性来确定网络实例中什么变量可以学习。
set_inpt 方法用来设置该层的输入,并计算相应的输出。我使用 inpt 而非 input 因为在python 中 input 是一个内置函数。如果将两者混淆,必然会导致不可预测的行为,对出现的问题也难以定位。注意我们实际上用两种方式设置输入的:self.input 和 self.inpt_dropout。因为训练时我们可能要使用 dropout。如果使用 dropout,就需要设置对应丢弃的概率 self.p_dropout。这就是在set_inpt 方法的倒数第二行 dropout_layer 做的事。所以 self.inpt_dropout 和 self.output_dropout在训练过程中使用,而 self.inpt 和 self.output 用作其他任务,比如衡量验证集和测试集模型的准确度。
ConvPoolLayer 和 SoftmaxLayer 类定义和 FullyConnectedLayer 定义差不多。所以我这儿不会给出代码。如果你感兴趣,可以参考本节后面的 network3.py 的代码。
尽管这样,我们还是指出一些重要的微弱的细节差别。明显一点的是,在 ConvPoolLayer 和 SoftmaxLayer 中,我们采用了相应的合适的计算输出激活值方式。幸运的是,Theano 提供了内置的操作让我们计算卷积、max-pooling 和 softmax 函数。
不大明显的,在我们引入softmax layer 时,我们没有讨论如何初始化权重和偏差。其他地方我们已经讨论过对 sigmoid 层,我们应当使用合适参数的正态分布来初始化权重。但是这个启发式的论断是针对 sigmoid 神经元的(做一些调整可以用于 tanh 神经元上)。但是,并没有特殊的原因说这个论断可以用在 softmax 层上。所以没有一个先验的理由应用这样的初始化。与其使用之前的方法初始化,我这里会将所有权值和偏差设置为 $$0$$。这是一个 ad hoc 的过程,但在实践使用过程中效果倒是很不错。
好了,我们已经看过了所有关于层的类。那么 Network 类是怎样的呢?让我们看看 __init__ 方法:
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Takes a list of `layers`, describing the network architecture, and
a value for the `mini_batch_size` to be used during training
by stochastic gradient descent.
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropout这段代码大部分是可以自解释的。self.params = [param for layer in ...] 此行代码对每层的参数捆绑到一个列表中。Network.SGD 方法会使用 self.params 来确定 Network 中哪些变量需要学习。而 self.x = T.matrix("x") 和 self.y = T.ivector("y") 则定义了 Theano 符号变量 x 和 y。这些会用来表示输入和网络得到的输出。
这儿不是 Theano 的教程,所以不会深度讨论这些变量指代什么东西。但是粗略的想法就是这些代表了数学变量,而非显式的值。我们可以对这些变量做通常需要的操作:加减乘除,作用函数等等。实际上,Theano 提供了很多对符号变量进行操作方法,如卷积、max-pooling等等。但是最重要的是能够进行快速符号微分运算,使用 BP 算法一种通用的形式。这对于应用随机梯度下降在若干种网络结构的变体上特别有效。特别低,接下来几行代码定义了网络的符号输出。我们通过下面这行
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)设置初始层的输入。
请注意输入是以每次一个 mini-batch 的方式进行的,这就是 mini-batch size 为何要指定的原因。还需要注意的是,我们将输入 self.x 传了两次:这是因为我们我们可能会以两种方式(有dropout和无dropout)使用网络。for 循环将符号变量 self.x 通过 Network 的层进行前向传播。这样我们可以定义最终的输出 output 和 output_dropout 属性,这些都是 Network 符号式输出。
现在我们理解了 Network 是如何初始化了,让我们看看它如何使用 SGD 方法进行训练的。代码看起来很长,但是它的结构实际上相当简单。代码后面也有一些注解。
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Train the network using mini-batch stochastic gradient descent."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# compute number of minibatches for training, validation and testing
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# define functions to train a mini-batch, and to compute the
# accuracy in validation and test mini-batches.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Do the actual training
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration % 1000 == 0:
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1) % num_training_batches == 0:
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2%}".format(
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2%}'.format(
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))前面几行很直接,将数据集分解成 x 和 y 两部分,并计算在每个数据集中 mini-batch 的数量。接下来的几行更加有意思,这也体现了 Theano 有趣的特性。那么我们就摘录详解一下:
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\ 0.5*lambda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad) for param, grad in zip(self.params, grads)]这几行,我们符号化地给出了规范化的 log-likelihood 代价函数,在梯度函数中计算了对应的导数,以及对应参数的更新方式。Theano 让我们通过这短短几行就能够获得这些效果。唯一隐藏的是计算 cost 包含一个对输出层 cost 方法的调用;该代码在 network3.py 中其他地方。但是,总之代码很短而且简单。有了所有这些定义好的东西,下面就是定义 train_mini_batch 函数,该 Theano 符号函数在给定 minibatch 索引的情况下使用 updates 来更新 Network 的参数。类似地,validate_mb_accuracy 和 test_mb_accuracy 计算在任意给定的 minibatch 的验证集和测试集合上 Network 的准确度。通过对这些函数进行平均,我们可以计算整个验证集和测试数据集上的准确度。
SGD 方法剩下的就是可以自解释的了——我们对次数进行迭代,重复使用 训练数据的 minibatch 来训练网络,计算验证集和测试集上的准确度。
好了,我们已经理解了 network3.py 代码中大多数的重要部分。让我们看看整个程序,你不需过分仔细地读下这些代码,但是应该享受粗看的过程,并随时深入研究那些激发出你好奇地代码段。理解代码的最好的方法就是通过修改代码,增加额外的特征或者重新组织那些你认为能够更加简洁地完成的代码。代码后面,我们给出了一些对初学者的建议。这儿是代码:
在 GPU 上使用 Theano 可能会有点难度。特别地,很容在从 GPU 中拉取数据时出现错误,这可能会让运行变得相当慢。我已经试着避免出现这样的情况,但是也不能肯定在代码扩充后出现一些问题。对于你们遇到的问题或者给出的意见我洗耳恭听(mn@michaelnielsen.org)。
"""network3.py
~~~~~~~~~~~~~~
A Theano-based program for training and running simple neural
networks.
Supports several layer types (fully connected, convolutional, max
pooling, softmax), and activation functions (sigmoid, tanh, and
rectified linear units, with more easily added).
When run on a CPU, this program is much faster than network.py and
network2.py. However, unlike network.py and network2.py it can also
be run on a GPU, which makes it faster still.
Because the code is based on Theano, the code is different in many
ways from network.py and network2.py. However, where possible I have
tried to maintain consistency with the earlier programs. In
particular, the API is similar to network2.py. Note that I have
focused on making the code simple, easily readable, and easily
modifiable. It is not optimized, and omits many desirable features.
This program incorporates ideas from the Theano documentation on
convolutional neural nets (notably,
http://deeplearning.net/tutorial/lenet.html ), from Misha Denil's
implementation of dropout (https://github.com/mdenil/dropout ), and
from Chris Olah (http://colah.github.io ).
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
import theano
import theano.tensor as T
from theano.tensor.nnet import conv
from theano.tensor.nnet import softmax
from theano.tensor import shared_randomstreams
from theano.tensor.signal import downsample
# Activation functions for neurons
def linear(z): return z
def ReLU(z): return T.maximum(0.0, z)
from theano.tensor.nnet import sigmoid
from theano.tensor import tanh
#### Constants
GPU = True
if GPU:
print "Trying to run under a GPU. If this is not desired, then modify "+\
"network3.py\nto set the GPU flag to False."
try: theano.config.device = 'gpu'
except: pass # it's already set
theano.config.floatX = 'float32'
else:
print "Running with a CPU. If this is not desired, then the modify "+\
"network3.py to set\nthe GPU flag to True."
#### Load the MNIST data
def load_data_shared(filename="../data/mnist.pkl.gz"):
f = gzip.open(filename, 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
def shared(data):
"""Place the data into shared variables. This allows Theano to copy
the data to the GPU, if one is available.
"""
shared_x = theano.shared(
np.asarray(data[0], dtype=theano.config.floatX), borrow=True)
shared_y = theano.shared(
np.asarray(data[1], dtype=theano.config.floatX), borrow=True)
return shared_x, T.cast(shared_y, "int32")
return [shared(training_data), shared(validation_data), shared(test_data)]
#### Main class used to construct and train networks
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Takes a list of `layers`, describing the network architecture, and
a value for the `mini_batch_size` to be used during training
by stochastic gradient descent.
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropout
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Train the network using mini-batch stochastic gradient descent."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# compute number of minibatches for training, validation and testing
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# define functions to train a mini-batch, and to compute the
# accuracy in validation and test mini-batches.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Do the actual training
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration % 1000 == 0:
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1) % num_training_batches == 0:
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2%}".format(
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2%}'.format(
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))
#### Define layer types
class ConvPoolLayer(object):
"""Used to create a combination of a convolutional and a max-pooling
layer. A more sophisticated implementation would separate the
two, but for our purposes we'll always use them together, and it
simplifies the code, so it makes sense to combine them.
"""
def __init__(self, filter_shape, image_shape, poolsize=(2, 2),
activation_fn=sigmoid):
"""`filter_shape` is a tuple of length 4, whose entries are the number
of filters, the number of input feature maps, the filter height, and the
filter width.
`image_shape` is a tuple of length 4, whose entries are the
mini-batch size, the number of input feature maps, the image
height, and the image width.
`poolsize` is a tuple of length 2, whose entries are the y and
x pooling sizes.
"""
self.filter_shape = filter_shape
self.image_shape = image_shape
self.poolsize = poolsize
self.activation_fn=activation_fn
# initialize weights and biases
n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
self.w = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape),
dtype=theano.config.floatX),
borrow=True)
self.b = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)),
dtype=theano.config.floatX),
borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape(self.image_shape)
conv_out = conv.conv2d(
input=self.inpt, filters=self.w, filter_shape=self.filter_shape,
image_shape=self.image_shape)
pooled_out = downsample.max_pool_2d(
input=conv_out, ds=self.poolsize, ignore_border=True)
self.output = self.activation_fn(
pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
self.output_dropout = self.output # no dropout in the convolutional layers
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
class SoftmaxLayer(object):
def __init__(self, n_in, n_out, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.zeros((n_in, n_out), dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.zeros((n_out,), dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b)
def cost(self, net):
"Return the log-likelihood cost."
return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y])
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
#### Miscellanea
def size(data):
"Return the size of the dataset `data`."
return data[0].get_value(borrow=True).shape[0]
def dropout_layer(layer, p_dropout):
srng = shared_randomstreams.RandomStreams(
np.random.RandomState(0).randint(999999))
mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape)
return layer*T.cast(mask, theano.config.floatX)问题
-
目前,
SGD方法需要用户手动确定训练的次数(epoch)。早先在本书中,我们讨论了一种自动选择训练次数的方法,也就是early stopping。修改network3.py以实现 Early stopping。 -
增加一个
Network方法来返回在任意数据集上的准确度。 -
修改
SGD方法来允许学习率 $$\eta$$ 可以是训练次数的函数。提示:在思考这个问题一段时间后,你可能会在this link 找到有用的信息。 -
在本章前面我曾经描述过一种通过应用微小的旋转、扭曲和变化来扩展训练数据的方法。改变
network3.py来加入这些技术。注意:除非你有充分多的内存,否则显式地产生整个扩展数据集是不大现实的。所以要考虑一些变通的方法。 -
在
network3.py中增加load和save方法。 -
当前的代码缺点就是只有很少的用来诊断的工具。你能想出一些诊断方法告诉我们网络过匹配到什么程度么?加上这些方法。
-
我们已经对rectified linear unit 及 sigmoid 和 tanh 函数神经元使用了同样的初始方法。正如这里所说,这种初始化方法只是适用于 sigmoid 函数。假设我们使用一个全部使用 RLU 的网络。试说明以常数 $$c$$ 倍调整网络的权重最终只会对输出有常数 $$c$$ 倍的影响。如果最后一层是 softmax,则会发生什么样的变化?对 RLU 使用 sigmoid 函数的初始化方法会怎么样?有没有更好的初始化方法?注意:这是一个开放的问题,并不是说有一个简单的自包含答案。还有,思考这个问题本身能够帮助你更好地理解包含 RLU 的神经网络。
- 我们对于不稳定梯度问题的分析实际上是针对 sigmoid 神经元的。如果是 RLU,那分析又会有什么差异?你能够想出一种使得网络不太会受到不稳定梯度问题影响的好方法么?注意:好实际上就是一个研究性问题。实际上有很多容易想到的修改方法。但我现在还没有研究足够深入,能告诉你们什么是真正的好技术。
图像识别领域中的近期进展
在 1998 年,MNIST 数据集被提出来,那时候需要花费数周能够获得一个最优的模型,和我们现在使用 GPU 在少于 1 小时内训练的模型性能差很多。所以,MNIST 已经不是一个能够推动技术边界前进的问题了;不过,现在的训练速度让 MNIST 能够成为教学和学习的样例。同时,研究重心也已经发生了转变,现代的研究工作包含更具挑战性的图像识别问题。在本节,我们简短介绍一些近期使用神经网络进行图像识别上的研究进展。
本节内容和本书其他大部分都不一样。整本书,我都专注在那些可能会成为持久性的方法上——诸如 BP、规范化、和卷积网络。我已经尽量避免提及那些在我写书时很热门但长期价值未知的研究内容了。在科学领域,这样太过热门容易消逝的研究太多了,最终对科学发展的价值却是很微小的。所以,可能会有人怀疑:“好吧,在图像识别中近期的发展就是这种情况么?两到三年后,事情将发生变化。所以,肯定这些结果仅仅是一些想在研究前沿阵地领先的专家的专属兴趣而已?为何又费力来讨论这个呢?”
这种怀疑是正确的,近期研究论文中一些改良的细节最终会失去其自身的重要性。过去几年里,我们已经看到了使用深度学习解决特别困难的图像识别任务上巨大进步。假想一个科学史学者在 2100 年写起计算机视觉。他们肯定会将 2011 到 2015(可能再加上几年)这几年作为使用深度卷积网络获得重大突破的时段。但这并不意味着深度卷积网络,还有dropout、RLU等等,在 2100 年仍在使用。但这确实告诉我们在思想的历史上,现在,正发生着重要的转变。这有点像原子的发现,抗生素的发明:在历史的尺度上的发明和发现。所以,尽管我们不会深入这些细节,但仍值得从目前正在发生的研究成果中获得一些令人兴奋的研究发现。
The 2012 LRMD paper:让我们从一篇来自 Stanford 和 Google 的研究者的论文开始。后面将这篇论文简记为 LRMD,前四位作者的姓的首字母命名。LRMD 使用神经网络对 ImageNet 的图片进行分类,这是一个具有非常挑战性的图像识别问题。2011 年 ImageNet 数据包含了 $$16,000,000$$ 的全色图像,有 $$20,000$$ 个类别。图像从开放的网络上爬去,由 Amazon Mechanical Turk 服务的工人分类。下面是几幅 ImageNet 的图像:

上面这些分别属于 圆线刨,棕色烂根须,加热的牛奶,及 通常的蚯蚓。如果你想挑战一下,你可以访问hand tools,里面包含了一系列的区分的任务,比如区分 圆线刨、短刨、倒角刨以及其他十几种类型的刨子和其他的类别。我不知道读者你是怎么样一个人,但是我不能将所有这些工具类型都确定地区分开。这显然是比 MNIST 任务更具挑战性的任务。LRMD 网络获得了不错的 15.8% 的准确度。这看起很不给力,但是在先前最优的 9.3% 准确度上却是一个大的突破。这个飞跃告诉人们,神经网络可能会成为一个对非常困难的图像识别任务的强大武器。
The 2012 KSH paper:在 2012 年,出现了一篇 LRMD 后续研究 Krizhevsky, Sutskever and Hinton (KSH)。KSH 使用一个受限 ImageNet 的子集数据训练和测试了一个深度卷积神经网络。这个数据集是机器学习竞赛常用的一个数据集——ImageNet Large-Scale Visual Recognition Challenge(ILSVRC)。使用一个竞赛数据集可以方便比较神经网络和其他方法之间的差异。ILSVRC-2012 训练集包含 $$120,000$$ 幅 ImageNet 的图像,共有 $$1,000$$ 类。验证集和测试集分别包含 $$50,000$$ 和 $$150,000$$ 幅,也都是同样的 $$1,000$$ 类。
ILSVRC 竞赛中一个难点是许多图像中包含多个对象。假设一个图像展示出一只拉布拉多犬追逐一只足球。所谓“正确的”分类可能是拉布拉多犬。但是算法将图像归类为足球就应该被惩罚么?由于这样的模糊性,我们做出下面设定:如果实际的ImageNet分类是出于算法给出的最可能的 5 类,那么算法最终被认为是正确的。KSH 深度卷积网络达到了 84.7% 的准确度,比第二名的 73.8% 高出很多。使用更加严格度量,KSH 网络业达到了 63.3% 的准确度。
我们这里会简要说明一下 KSH 网络,因为这是后续很多工作的源头。而且它也和我们之前给出的卷积网络相关,只是更加复杂精细。KSH 使用深度卷积网络,在两个 GPU 上训练。使用两个 GPU 因为 GPU 的型号使然(NVIDIA GeForce GTX 580 没有足够大的内存来存放整个网络)所以用这样的方式进行内存的分解。
KSH 网络有 $$7$$ 个隐藏层。前 $$5$$ 个隐藏层是卷积层(可能会包含 max-pooling),而后两个隐藏层则是全连接层。输出层则是 $$1,000$$ 的 softmax,对应于 $$1,000$$ 种分类。下面给出了网络的架构图,来自 KSH 的论文。我们会给出详细的解释。注意很多层被分解为 $$2$$ 个部分,对应于 $$2$$ 个 GPU。
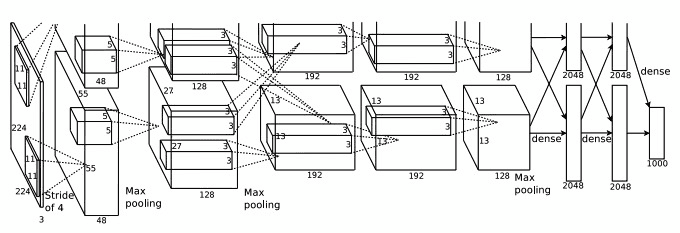
输出层包含 $$3\times 224\times 224$$ 神经元,表示一幅 $$224\times 224$$ 的图像的RGB 值。回想一下,ImageNet 包含不同分辨率的图像。这里也会有问题,因为神经网络输入层通常是固定的大小。KSH 通过将每幅图进行的重设定,使得短的边长度为 256。然后在重设后的图像上裁剪出 $$256\times 256$$ 的区域。最终 KSH 从 $$256\times 256$$ 的图像中抽取出随机的 $$224\times 224$$ 的子图(和水平反射)。他们使用随机的方式,是为了扩展训练数据,这样能够缓解过匹配的情况。在大型网络中这样的方法是很有效的。这些 $$224 \times 224$$ 的图像就成为了网络的输入。在大多数情形下,裁剪的图像仍会包含原图中主要的对象。
现在看看 KSH 的隐藏层,第一隐藏层是一个卷积层,还有 max-pooling。使用了大小为 $$11\times 11$$ 的局部感应区,和大小为 $$4$$ 的步长。总共有 $$96$$ 个特征映射。特征映射被分成两份,分别存放在两块 GPU 上。max-pooling 在这层和下层都是 $$3\times 3$$ 区域进行,由于允许使用重叠的 pooling 区域,pooling 层其实会产生两个像素值。
Pooling layers in CNNs summarize the outputs of neighboring groups of neurons in the same kernel map. Traditionally, the neighborhoods summarized by adjacent pooling units do not overlap (e.g., [17, 11, 4]). To be more precise, a pooling layer can be thought of as consisting of a grid of pooling units spaced s pixels apart, each summarizing a neighborhood of size z × z centered at the location of the pooling unit. If we set s = z, we obtain traditional local pooling as commonly employed in CNNs. If we set s < z, we obtain overlapping pooling. This is what we use throughout our network, with s = 2 and z = 3. This scheme reduces the top-1 and top-5 error rates by 0.4% and 0.3%, respectively, as compared with the non-overlapping scheme s = 2, z = 2, which produces output of equivalent dimensions. We generally observe during training that models with overlapping pooling find it slightly more difficult to overfit.
第二隐藏层同样是卷积层,并附加一个 max-pooling 步骤。使用了 $$5 \times 5$$ 的局部感知区,总共有 $$256$$ 个特征映射,在每个 GPU 上各分了 $$128$$ 个。注意到,特征映射只使用 $$48$$ 个输入信道,而不是前一层整个 $$96$$ 个输出。这是因为任何单一的特征映射仅仅使用来自同一个 GPU 的输入。从这个角度看,这个网络和此前我们使用的卷积网络结构还是不同的,尽管本质上仍一致。
第三、四和五隐藏层也是卷积层,但和前两层不同的是:他们不包含 max-pooling 步。各层参数分别是:(3)$$384$$ 个特征映射,$$3\times 3$$ 的局部感知区,$$256$$ 个输入信道;(4)$$384$$ 个特征映射,其中 $$3 \times 3$$ 的局部感知区和 $$192$$ 个输入信道;(5)$$256$$ 个特征映射,$$3\times 3$$ 的局部感知区,和 $$192$$ 个输入信道。注意第三层包含一些 GPU 间的通信(如图所示)这样可使得特征映射能够用上所有 $$256$$ 个输入信道。
第六、七隐藏层是全连接层,其中每层有 $$4,096$$ 个神经元。
输出层是一个 $$1,000$$ 个单元的 softmax 层。
KSH 网络使用了很多的技术。放弃了 sigmoid 或者 tanh 激活函数的使用, KSH 全部采用 RLU,显著地加速了训练过程。KSH 网络用有将近 $$60,000,000$$ 的参数,所以,就算有大规模的数据训练,也可能出现过匹配情况。为了克服这个缺点,作者使用了随机剪裁策略扩展了训练数据集。另外还通过使用 l2 regularization的变体和 dropuout 来克服过匹配。网络本身使用 基于momentum 的 mini-batch 随机梯度下降进行训练。
这就是 KSH 论文中诸多核心想法的概述。细节我们不去深究,你可以通过仔细阅读论文获得。或者你也可以参考 Alexandrite Krizhevsky 的cuda-convnet 及后续版本,这里包含了这些想法的实现。还有基于 Theano 的实现也可以在这儿找到。尽管使用多 GPU 会让情况变得复杂,但代码本身还是类似于之前我们写出来的那些。Caffe 神经网络框架也有一个 KSH 网络的实现,看Model Zoo。
The 2014 ILSVRC 竞赛:2012年后,研究一直在快速推进。看看 2014年的 ILSVRC 竞赛。和 2012 一样,这次也包括了一个 $$120,000$$ 张图像,$$1,000$$ 种类别,而最终评价也就是看网络输出前五是不是包含正确的分类。胜利的团队,基于 Google 之前给出的结果,使用了包含 $$22$$ 层的深度卷积网络。他们称此为 GoogLeNet,向 LeNet-5 致敬。GoogLeNet 达到了93.33% 的准确率远超2013年的 88.3% Clarifai 和 2012 年的KSH 84.7%。
那么 GoogLeNet 93.33% 的准确率又是多好呢?在2014年,一个研究团队写了一篇关于 ILSVRC 竞赛的综述文章。其中有个问题是人类在这个竞赛中能表现得如何。为了做这件事,他们构建了一个系统让人类对 ILSVRC 图像进行分类。其作者之一 Andrej Karpathy 在一篇博文中解释道,让人类达到 GoogLeNet 的性能确实很困难:
...the task of labeling images with 5 out of 1000 categories quickly turned out to be extremely challenging, even for some friends in the lab who have been working on ILSVRC and its classes for a while. First we thought we would put it up on [Amazon Mechanical Turk]. Then we thought we could recruit paid undergrads. Then I organized a labeling party of intense labeling effort only among the (expert labelers) in our lab. Then I developed a modified interface that used GoogLeNet predictions to prune the number of categories from 1000 to only about 100. It was still too hard - people kept missing categories and getting up to ranges of 13-15% error rates. In the end I realized that to get anywhere competitively close to GoogLeNet, it was most efficient if I sat down and went through the painfully long training process and the subsequent careful annotation process myself... The labeling happened at a rate of about 1 per minute, but this decreased over time... Some images are easily recognized, while some images (such as those of fine-grained breeds of dogs, birds, or monkeys) can require multiple minutes of concentrated effort. I became very good at identifying breeds of dogs... Based on the sample of images I worked on, the GoogLeNet classification error turned out to be 6.8%... My own error in the end turned out to be 5.1%, approximately 1.7% better.
换言之,一个专家级别的人类,非常艰难地检查图像,付出很大的精力才能够微弱胜过深度神经网络。实际上,Karpathy 指出第二个人类专家,用小点的图像样本训练后,只能达到 12.0% 的 top-5 错误率,明显弱于 GoogLeNet。大概有一半的错误都是专家“难以发现和认定正确的类别究竟是什么”。
这些都是惊奇的结果。根据这项工作,很多团队也报告 top-5 错误率实际上好过 5.1%。有时候,在媒体上被报道成系统有超过人类的视觉。尽管这项发现是很振奋人心的,但是这样的报道只能算是一种误解,认为系统在视觉上超过了人类,事实上并非这样。ILSVRC 竞赛问题在很多方面都是受限的——在公开的网络上获得图像并不具备在实际应用中的代表性!而且 top-5 标准也是非常人工设定的。我们在图像识别,或者更宽泛地说,计算机视觉方面的研究,还有很长的路要走。当然看到近些年的这些进展,还是很鼓舞人心的。
其他研究活动:上面关注于 ImageNet,但是也还有一些其他的使用神经网络进行图像识别的工作。我们也介绍一些进展。
一个鼓舞人心的应用上的结果就是 Google 的一个团队做出来的,他们应用深度卷积网络在识别 Google 的街景图像库中街景数字上。在他们的论文中,对接近 $$100,000,000$$ 街景数字的自动检测和自动转述已经能打到与人类不相上下的程度。系统速度很快:在一个小时内将法国所有的街景数字都转述了。他们说道:“拥有这种新数据集能够显著提高 Google Maps 在一些国家的地理精准度,尤其是那些缺少地理编码的地区。”他们还做了一个更一般的论断:“我们坚信这个模型,已经解决了很多应用中字符短序列的 OCR 问题。 ”
我可能已经留下了印象——所有的结果都是令人兴奋的正面结果。当然,目前一些有趣的研究工作也报道了一些我们还没能够真的理解的根本性的问题。例如,2013 年一篇论文指出,深度网络可能会受到有效忙点的影响。看看下面的图示。左侧是被网络正确分类的 ImageNet 图像。右边是一幅稍受干扰的图像(使用中间的噪声进行干扰)结果就没有能够正确分类。作者发现对每幅图片都存在这样的“对手”图像,而非少量的特例。

这是一个令人不安的结果。论文使用了基于同样的被广泛研究使用的 KSH 代码。尽管这样的神经网络计算的函数在理论上都是连续的,结果表明在实际应用中,可能会碰到很多非常不连续的函数。更糟糕的是,他们将会以背离我们直觉的方式变得不连续。真是烦心啊。另外,现在对这种不连续性出现的原因还没有搞清楚:是跟损失函数有关么?或者激活函数?又或是网络的架构?还是其他?我们一无所知。
现在,这些问题也没有听起来这么吓人。尽管对手图像会出现,但是在实际场景中也不常见。正如论文指出的那样:
对手反例的存在看起来和网络能获得良好的泛化性能相违背。实际上,如果网络可以很好地泛化,会受到这些难以区分出来的对手反例怎么样的影响?解释是,对手反例集以特别低的概率出现,因此在测试集中几乎难以发现,然而对手反例又是密集的(有点像有理数那样),所以会在每个测试样本附近上出现。
我们对神经网络的理解还是太少了,这让人觉得很沮丧,上面的结果仅仅是近期的研究成果。当然了,这样结果带来一个主要好处就是,催生出一系列的研究工作。例如,最近一篇文章说明,给定一个训练好的神经网络,可以产生对人类来说是白噪声的图像,但是网络能够将其确信地分类为某一类。这也是我们需要追寻的理解神经网络和图像识别应用上的研究方向。
虽然遇到这么多的困难,前途倒还是光明的。我们看到了在众多相当困难的基准任务上快速的研究进展。同样还有实际问题的研究进展,例如前面提到的街景数字的识别。但是需要注意的是,仅仅看到在那些基准任务,乃至实际应用的进展,是不够的。因为还有很多根本性的现象,我们对其了解甚少,就像对手图像的存在问题。当这样根本性的问题还亟待发现(或者解决)时,盲目地说我们已经接近最终图像识别问题的答案就很不合适了。这样的根本问题当然也会催生出不断的后续研究。
其他的深度学习模型
在整本书中,我们聚焦在解决 MNIST 数字分类问题上。这一“下金蛋的”问题让我们深入理解了一些强大的想法:随机梯度下降,BP,卷积网络,正规化等等。但是该问题却也是相当狭窄的。如果你研读过神经网络的研究论文,那么会遇到很多这本书中未曾讨论的想法:RNN,Boltzmann Machine,生成式模型,迁移学习,强化学习等等……等等!(太多了)神经网络是一个广阔的领域。然而,很多重要的想法都是我们书中探讨过的那些想法的变种,在有了本书的知识基础上,可能需要一些额外的努力,便可以理解这些新的想法了。所以在本节,我们给出这些想法的一些介绍。介绍本身不会非常细节化,可能也不会很深入——倘若要达成这两点,这本书就得扩展相当多内容了。因此,我们接下来的讨论是偏重思想性的启发,尝试去激发这个领域的产生丰富的概念,并将一些丰富的想法关联于前面已经介绍过的概念。我也会提供一些其他学习资源的连接。当然,链接给出的很多想法也会很快被超过,所以推荐你学会搜索最新的研究成果。尽管这样,我还是很期待众多本质的想法能够受到足够久的关注。
Recurrent Neural Networks (RNNs):在前馈神经网络中,单独的输入完全确定了剩下的层上的神经元的激活值。可以想象,这是一幅静态的图景:网络中的所有事物都被固定了,处于一种“冰冻结晶”的状态。但假如,我们允许网络中的元素能够以动态方式不断地比那话。例如,隐藏神经元的行为不是完全由前一层的隐藏神经元,而是同样受制于更早的层上的神经元的激活值。这样肯定会带来跟前馈神经网络不同的效果。也可能隐藏和输出层的神经元的激活值不会单单由当前的网络输入决定,而且包含了前面的输入的影响。
拥有之类时间相关行为特性的神经网络就是递归神经网络,常写作 RNN。当然有不同的方式来从数学上给出 RNN 的形式定义。你可以参考维基百科上的RNN介绍来看看 RNN。在我写作本书的时候,维基百科上介绍了超过 13 种不同的模型。但除了数学细节,更加一般的想法是,RNN 是某种体现出了随时间动态变化的特性的神经网络。也毫不奇怪,RNN 在处理时序数据和过程上效果特别不错。这样的数据和过程正是语音识别和自然语言处理中常见的研究对象。
RNN 被用来将传统的算法思想,比如说 Turing 机或者编程语言,和神经网络进行联系上。这篇 2014 年的论文提出了一种 RNN 可以以 python 程序的字符级表达作为输入,用这个表达来预测输出。简单说,网络通过学习来理解某些 python 的程序。第二篇论文 同样是 2014 年的,使用 RNN 来设计一种称之为 “神经 Turing 机” 的模型。这是一种通用机器整个结构可以使用梯度下降来训练。作者训练 NTM 来推断对一些简单问题的算法,比如说排序和复制。
不过正如在文中提到的,这些例子都是极其简单的模型。学会执行 print(398345+42598) 并不能让网络称为一个正常的python解释器!对于这些想法,我们能推进得多远也是未知的。结果都充满了好奇。历史上,神经网络已经在传统算法上失败的模式识别问题上取得了一些成功。另外,传统的算法也在神经网络并不擅长的领域里占据上风。今天没有人会使用神经网络来实现 Web 服务器或者数据库程序。研究出将神经网络和传统的算法结合的模型一定是非常棒的。RNN 和 RNN 给出的启发可能会给我们不少帮助。
RNN 同样也在其他问题的解决中发挥着作用。在语音识别中,RNN 是特别有效的。例如,基于 RNN 的方法,已经在音位识别中取得了准确度的领先。同样在开发人类语言的上改进模型中得到应用。更好的语言模型意味着能够区分出发音相同的那些词。例如,好的语言模型,可以告诉我们“to infinity and beyond”比“two infinity and beyond”更可能出现,尽管两者的发音是相同的。RNN 在某些语言的标准测试集上刷新了记录。
在语音识别中的这项研究其实是包含于更宽泛的不仅仅是 RNN而是所有类型的深度神经网络的应用的一部分。例如,基于神经网络的方法在大规模词汇的连续语音识别中获得极佳的结果。另外,一个基于深度网络的系统已经用在了 Google 的 Android 操作系统中(详见Vincent Vanhoucke's 2012-2015 papers)
我刚刚讲完了 RNN 能做的一小部分,但还未提及他们如何工作。可能你并不诧异在前馈神经网络中的很多想法同样可以用在 RNN 中。尤其是,我们可以使用梯度下降和 BP 的直接的修改来训练 RNN。还有其他一些在前馈神经网络中的想法,如正规化技术,卷积和代价函数等都在 RNN 中非常有效。还有我们在书中讲到的很多技术都可以适配一下 RNN 场景。
Long Short-term Memory units(LSTMs):影响 RNN 的一个挑战是前期的模型会很难训练,甚至比前馈神经网络更难。原因就是我们在上一章提到的不稳定梯度的问题。回想一下,这个问题的通常表现就是在反向传播的时候梯度越变越小。这就使得前期的层学习非常缓慢。在 RNN 中这个问题更加糟糕,因为梯度不仅仅通过层反向传播,还会根据时间进行反向传播。如果网络运行了一段很长的时间,就会使得梯度特别不稳定,学不到东西。幸运的是,可以引入一个成为 long short-term memory 的单元进入 RNN 中。LSTM 最早是由 Hochreiter 和 Schmidhuber 在 1997 年提出,就是为了解决这个不稳定梯度的问题。LSTM 让 RNN 训练变得相当简单,很多近期的论文(包括我在上面给出的那些)都是用了 LSTM 或者相关的想法。
