权重初始化
创建了神经网络后,我们需要进行权重和偏差的初始化。到现在,我们一直是根据在第一章中介绍的那样进行初始化。提醒你一下,之前的方式就是根据独立的均值为 $$0$$,标准差为 $$1$$ 的高斯随机变量随机采样作为权重和偏差的初始值。这个方法工作的还不错,但是非常 ad hoc,所以我们需要寻找一些更好的方式来设置我们网络的初始化权重和偏差,这对于帮助网络学习速度的提升很有价值。
结果表明,我们可以比使用正规化的高斯分布效果更好。为什么?假设我们使用一个很多的输入神经元,比如说 $$1000$$。假设,我们已经使用正规化的高斯分布初始化了连接第一隐藏层的权重。现在我将注意力集中在这一层的连接权重上,忽略网络其他部分:
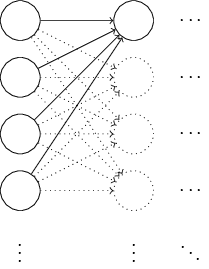
我们为了简化,假设,我们使用训练样本 x 其中一半的神经元值为 $$0$$,另一半为 $$1$$。下面的观点也是可以更加广泛地应用,但是你可以从特例中获得背后的思想。让我们考虑带权和 $$z=\sum_j w_j x_j + b$$ 的隐藏元输入。其中 $$500$$ 个项消去了,因为对应的输入 $$x_j=0$$。所以 $$z$$ 是 $$501$$ 个正规化的高斯随机变量的和,包含 $$500$$ 个权重项和额外的 $$1$$ 个偏差项。因此 $$z$$ 本身是一个均值为 $$0$$ 标准差为 $$\sqrt{501}\approx 22.4$$ 的分布。$$z$$ 其实有一个非常宽的高斯分布,不是非常尖的形状:

尤其是,我们可以从这幅图中看出 $$|z|$$ 会变得非常的大,比如说 $$z\gg1$$ 或者 $$z\ll 1$$。如果是这样,输出 $$\sigma(z)$$ 就会接近 $$1$$ 或者 $$0$$。也就表示我们的隐藏元会饱和。所以当出现这样的情况时,在权重中进行微小的调整仅仅会给隐藏元的激活值带来极其微弱的改变。而这种微弱的改变也会影响网络中剩下的神经元,然后会带来相应的代价函数的改变。结果就是,这些权重在我们进行梯度下降算法时会学习得非常缓慢。这其实和我们前面讨论的问题差不多,前面的情况是输出神经元在错误的值上饱和导致学习的下降。我们之前通过代价函数的选择解决了前面的问题。不幸的是,尽管那种方式在输出神经元上有效,但对于隐藏元的饱和却一点作用都没有。
我已经研究了第一隐藏层的权重输入。当然,类似的论断也对后面的隐藏层有效:如果权重也是用正规化的高斯分布进行初始化,那么激活值将会接近 $$0$$ 或者 $$1$$,学习速度也会相当缓慢。
还有可以帮助我们进行更好地初始化么,能够避免这种类型的饱和,最终避免学习速度的下降?假设我们有一个有 $$n{in}$$ 个输入权重的神经元。我们会使用均值为 $$0$$ 标准差为 $$1/\sqrt{n{in}}$$ 的高斯分布初始化这些权重。也就是说,我们会向下挤压高斯分布,让我们的神经元更不可能饱和。我们会继续使用均值为 $$0$$ 标准差为 $$1$$ 的高斯分布来对偏差进行初始化,后面会告诉你原因。有了这些设定,带权和 $$z=\sum_j w_j x_j + b$$ 仍然是一个均值为 $$0$$ 不过有很陡的峰顶的高斯分布。假设,我们有 $$500$$ 个值为 $$0$$ 的输入和$$500$$ 个值为 $$1$$ 的输入。那么很容证明 $$z$$ 是服从均值为 $$0$$ 标准差为 $$\sqrt{3/2} = 1.22$$ 的高斯分布。这图像要比以前陡得多,所以即使我已经对横坐标进行压缩为了进行更直观的比较:
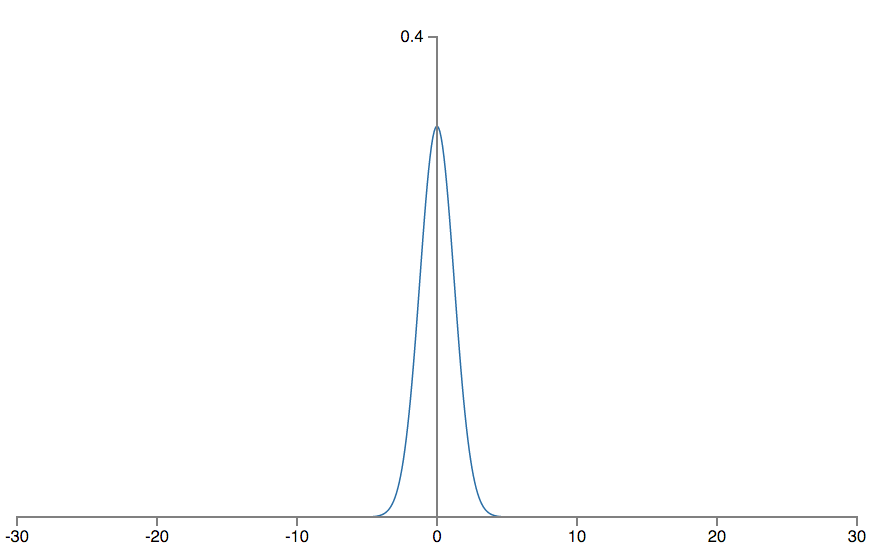
这样的一个神经元更不可能饱和,因此也不大可能遇到学习速度下降的问题。
练习
- 验证 $$z=\sum_j w_j x_j + b$$ 标准差为 $$\sqrt{3/2}$$。下面两点可能会有帮助:(a) 独立随机变量的和的方差是每个独立随即便方差的和;(b)方差是标准差的平方。
我在上面提到,我们使用同样的方式对偏差进行初始化,就是使用均值为 $$0$$ 标准差为 $$1$$ 的高斯分布来对偏差进行初始化。这其实是可行的,因为这样并不会让我们的神经网络更容易饱和。实际上,其实已经避免了饱和的问题的话,如何初始化偏差影响不大。有些人将所有的偏差初始化为 $$0$$,依赖梯度下降来学习合适的偏差。但是因为差别不是很大,我们后面还会按照前面的方式来进行初始化。
让我们在 MNIST 数字分类任务上比较一下新旧两种权重初始化方式。同样,还是使用 $$30$$ 个隐藏元,minibatch 的大小为 $$30$$,规范化参数 $$\lambda=5.0$$,然后是交叉熵代价函数。我们将学习率从 $$\eta=0.5$$ 调整到 $$0.1$$,因为这样会让结果在图像中表现得更加明显。我们先使用旧的初始化方法训练:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)我们也使用新方法来进行权重的初始化。这实际上还要更简单,因为 network2's 默认方式就是使用新的方法。这意味着我们可以丢掉 net.large_weight_initializer() 调用:
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)将结果用图展示出来,就是:
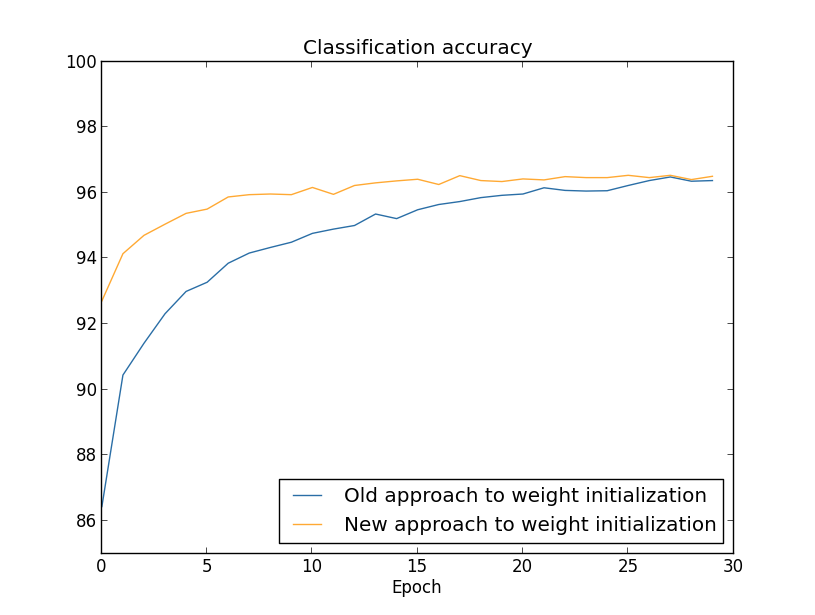
两种情形下,我们在 96% 的准确度上重合了。最终的分类准确度几乎完全一样。但是新的初始化技术带来了速度的提升。在第一种初始化方式的分类准确度在 87% 一下,而新的方法已经几乎达到了 93%。看起来的情况就是我们新的关于权重初始化的方式将训练带到了一个新的境界,让我们能够更加快速地得到好的结果。同样的情况在 $$100$$ 个神经元的设定中也出现了:

在这个情况下,两个曲线并没有重合。然而,我做的实验发现了其实就在一些额外的回合后(这里没有展示)准确度其实也是几乎相同的。所以,基于这些实验,看起来提升的权重初始化仅仅会加快训练,不会改变网络的性能。然而,在第四张,我们会看到一些例子里面使用 $$1/\sqrt{n_{in}}$$ 权重初始化的长期运行的结果要显著更优。因此,不仅仅能够带来训练速度的加快,有时候在最终性能上也有很大的提升。
$$1/\sqrt{n{in}}$$ 的权重初始化方法帮助我们提升了神经网络学习的方式。其他的权重初始化技术同样也有,很多都是基于这个基本的思想。我不会在这里给出其他的方法,因为 $$1/\sqrt{n{in}}$$ 已经可以工作得很好了。如果你对另外的思想感兴趣,我推荐你看看在 $$2012$$ 年的 Yoshua Bengio 的论文的 $$14$$ 和 $$15$$ 页,以及相关的参考文献。
Practical Recommendations for Gradient-Based Training of Deep Architectures, by Yoshua Bengio (2012).
问题
- 将规范化和改进的权重初始化方法结合使用 L2 规范化有时候会自动给我们一些类似于新的初始化方法的东西。假设我们使用旧的初始化权重的方法。考虑一个启发式的观点:(1)假设$$\lambda$$ 不太小,训练的第一回合将会几乎被权重下降统治。;(2)如果 $$\eta\lambda \ll n$$,权重会按照因子 $$exp(-\eta\lambda/m)$$ 每回合下降;(3)假设 $$\lambda$$ 不太大,权重下降会在权重降到 $$1/\sqrt{n}$$ 的时候保持住,其中 $$n$$ 是网络中权重的个数。用论述这些条件都已经满足本节给出的例子。
再看手写识别问题:代码
让我们实现本章讨论过的这些想法。我们将写出一个新的程序,network2.py,这是一个对第一章中开发的 network.py 的改进版本。如果你没有仔细看过 network.py,那你可能会需要重读前面关于这段代码的讨论。仅仅 $$74$$ 行代码,也很易懂。
和 network.py 一样,主要部分就是 Network 类了,我们用这个来表示神经网络。使用一个 sizes 的列表来对每个对应层进行初始化,默认使用交叉熵作为代价 cost 参数:
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=cost__init__ 方法的和 network.py 中一样,可以轻易弄懂。但是下面两行是新的,我们需要知道他们到底做了什么。
我们先看看 default_weight_initializer 方法,使用了我们新式改进后的初始化权重方法。如我们已经看到的,使用了均值为 $$0$$ 而标准差为 $$1/\sqrt{n}$$,$$n$$ 为对应的输入连接个数。我们使用均值为 $$0$$ 而标准差为 $$1$$ 的高斯分布来初始化偏差。下面是代码:
def default_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]为了理解这段代码,需要知道 np 就是进行线性代数运算的 Numpy 库。我们在程序的开头会 import Numpy。同样我们没有对第一层的神经元的偏差进行初始化。因为第一层其实是输入层,所以不需要引入任何的偏差。我们在 network.py 中做了完全一样的事情。
作为 default_weight_initializer 的补充,我们同样包含了一个 large_weight_initializer 方法。这个方法使用了第一章中的观点初始化了权重和偏差。代码也就仅仅是和default_weight_initializer差了一点点了:
def large_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]我将 larger_weight_initializer 方法包含进来的原因也就是使得跟第一章的结果更容易比较。我并没有考虑太多的推荐使用这个方法的实际情景。
初始化方法 __init__ 中的第二个新的东西就是我们初始化了 cost 属性。为了理解这个工作的原理,让我们看一下用来表示交叉熵代价的类:
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
return (a-y)让我们分解一下。第一个看到的是:即使使用的是交叉熵,数学上看,就是一个函数,这里我们用 Python 的类而不是 Python 函数实现了它。为什么这样做呢?答案就是代价函数在我们的网络中扮演了两种不同的角色。明显的角色就是代价是输出激活值 $$a$$ 和目标输出 $$y$$ 差距优劣的度量。这个角色通过 CrossEntropyCost.fn 方法来扮演。(注意,np.nan_to_num 调用确保了 Numpy 正确处理接近 $$0$$ 的对数值)但是代价函数其实还有另一个角色。回想第二章中运行反向传播算法时,我们需要计算网络输出误差,$$\delta^L$$。这种形式的输出误差依赖于代价函数的选择:不同的代价函数,输出误差的形式就不同。对于交叉熵函数,输出误差就如公式(66)所示:

所以,我们定义了第二个方法,CrossEntropyCost.delta,目的就是让网络知道如何进行输出误差的计算。然后我们将这两个组合在一个包含所有需要知道的有关代价函数信息的类中。
类似地,network2.py 还包含了一个表示二次代价函数的类。这个是用来和第一章的结果进行对比的,因为后面我们几乎都在使用交叉函数。代码如下。QuadraticCost.fn 方法是关于网络输出 $$a$$ 和目标输出 $$y$$ 的二次代价函数的直接计算结果。由 QuadraticCost.delta 返回的值就是二次代价函数的误差。
class QuadraticCost(object):
@staticmethod
def fn(a, y):
return 0.5*np.linalg.norm(a-y)**2
@staticmethod
def delta(z, a, y):
return (a-y) * sigmoid_prime(z)现在,我们理解了 network2.py 和 network.py 两个实现之间的主要差别。都是很简单的东西。还有一些更小的变动,下面我们会进行介绍,包含 L2 规范化的实现。在讲述规范化之前,我们看看 network2.py 完整的实现代码。你不需要太仔细地读遍这些代码,但是对整个结构尤其是文档中的内容的理解是非常重要的,这样,你就可以理解每段程序所做的工作。当然,你也可以随自己意愿去深入研究!如果你迷失了理解,那么请读读下面的讲解,然后再回到代码中。不多说了,给代码:
"""network2.py
~~~~~~~~~~~~~~
An improved version of network.py, implementing the stochastic
gradient descent learning algorithm for a feedforward neural network.
Improvements include the addition of the cross-entropy cost function,
regularization, and better initialization of network weights. Note
that I have focused on making the code simple, easily readable, and
easily modifiable. It is not optimized, and omits many desirable
features.
"""
#### Libraries
# Standard library
import json
import random
import sys
# Third-party libraries
import numpy as np
#### Define the quadratic and cross-entropy cost functions
class QuadraticCost(object):
@staticmethod
def fn(a, y):
"""Return the cost associated with an output ``a`` and desired output
``y``.
"""
return 0.5*np.linalg.norm(a-y)**2
@staticmethod
def delta(z, a, y):
"""Return the error delta from the output layer."""
return (a-y) * sigmoid_prime(z)
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
"""Return the cost associated with an output ``a`` and desired output
``y``. Note that np.nan_to_num is used to ensure numerical
stability. In particular, if both ``a`` and ``y`` have a 1.0
in the same slot, then the expression (1-y)*np.log(1-a)
returns nan. The np.nan_to_num ensures that that is converted
to the correct value (0.0).
"""
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
"""Return the error delta from the output layer. Note that the
parameter ``z`` is not used by the method. It is included in
the method's parameters in order to make the interface
consistent with the delta method for other cost classes.
"""
return (a-y)
#### Main Network class
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
"""The list ``sizes`` contains the number of neurons in the respective
layers of the network. For example, if the list was [2, 3, 1]
then it would be a three-layer network, with the first layer
containing 2 neurons, the second layer 3 neurons, and the
third layer 1 neuron. The biases and weights for the network
are initialized randomly, using
``self.default_weight_initializer`` (see docstring for that
method).
"""
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=cost
def default_weight_initializer(self):
"""Initialize each weight using a Gaussian distribution with mean 0
and standard deviation 1 over the square root of the number of
weights connecting to the same neuron. Initialize the biases
using a Gaussian distribution with mean 0 and standard
deviation 1.
Note that the first layer is assumed to be an input layer, and
by convention we won't set any biases for those neurons, since
biases are only ever used in computing the outputs from later
layers.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def large_weight_initializer(self):
"""Initialize the weights using a Gaussian distribution with mean 0
and standard deviation 1. Initialize the biases using a
Gaussian distribution with mean 0 and standard deviation 1.
Note that the first layer is assumed to be an input layer, and
by convention we won't set any biases for those neurons, since
biases are only ever used in computing the outputs from later
layers.
This weight and bias initializer uses the same approach as in
Chapter 1, and is included for purposes of comparison. It
will usually be better to use the default weight initializer
instead.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
lmbda = 0.0,
evaluation_data=None,
monitor_evaluation_cost=False,
monitor_evaluation_accuracy=False,
monitor_training_cost=False,
monitor_training_accuracy=False):
"""Train the neural network using mini-batch stochastic gradient
descent. The ``training_data`` is a list of tuples ``(x, y)``
representing the training inputs and the desired outputs. The
other non-optional parameters are self-explanatory, as is the
regularization parameter ``lmbda``. The method also accepts
``evaluation_data``, usually either the validation or test
data. We can monitor the cost and accuracy on either the
evaluation data or the training data, by setting the
appropriate flags. The method returns a tuple containing four
lists: the (per-epoch) costs on the evaluation data, the
accuracies on the evaluation data, the costs on the training
data, and the accuracies on the training data. All values are
evaluated at the end of each training epoch. So, for example,
if we train for 30 epochs, then the first element of the tuple
will be a 30-element list containing the cost on the
evaluation data at the end of each epoch. Note that the lists
are empty if the corresponding flag is not set.
"""
if evaluation_data: n_data = len(evaluation_data)
n = len(training_data)
evaluation_cost, evaluation_accuracy = [], []
training_cost, training_accuracy = [], []
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(
mini_batch, eta, lmbda, len(training_data))
print "Epoch %s training complete" % j
if monitor_training_cost:
cost = self.total_cost(training_data, lmbda)
training_cost.append(cost)
print "Cost on training data: {}".format(cost)
if monitor_training_accuracy:
accuracy = self.accuracy(training_data, convert=True)
training_accuracy.append(accuracy)
print "Accuracy on training data: {} / {}".format(
accuracy, n)
if monitor_evaluation_cost:
cost = self.total_cost(evaluation_data, lmbda, convert=True)
evaluation_cost.append(cost)
print "Cost on evaluation data: {}".format(cost)
if monitor_evaluation_accuracy:
accuracy = self.accuracy(evaluation_data)
evaluation_accuracy.append(accuracy)
print "Accuracy on evaluation data: {} / {}".format(
self.accuracy(evaluation_data), n_data)
print
return evaluation_cost, evaluation_accuracy, \
training_cost, training_accuracy
def update_mini_batch(self, mini_batch, eta, lmbda, n):
"""Update the network's weights and biases by applying gradient
descent using backpropagation to a single mini batch. The
``mini_batch`` is a list of tuples ``(x, y)``, ``eta`` is the
learning rate, ``lmbda`` is the regularization parameter, and
``n`` is the total size of the training data set.
"""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = (self.cost).delta(zs[-1], activations[-1], y)
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def accuracy(self, data, convert=False):
"""Return the number of inputs in ``data`` for which the neural
network outputs the correct result. The neural network's
output is assumed to be the index of whichever neuron in the
final layer has the highest activation.
The flag ``convert`` should be set to False if the data set is
validation or test data (the usual case), and to True if the
data set is the training data. The need for this flag arises
due to differences in the way the results ``y`` are
represented in the different data sets. In particular, it
flags whether we need to convert between the different
representations. It may seem strange to use different
representations for the different data sets. Why not use the
same representation for all three data sets? It's done for
efficiency reasons -- the program usually evaluates the cost
on the training data and the accuracy on other data sets.
These are different types of computations, and using different
representations speeds things up. More details on the
representations can be found in
mnist_loader.load_data_wrapper.
"""
if convert:
results = [(np.argmax(self.feedforward(x)), np.argmax(y))
for (x, y) in data]
else:
results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in data]
return sum(int(x == y) for (x, y) in results)
def total_cost(self, data, lmbda, convert=False):
"""Return the total cost for the data set ``data``. The flag
``convert`` should be set to False if the data set is the
training data (the usual case), and to True if the data set is
the validation or test data. See comments on the similar (but
reversed) convention for the ``accuracy`` method, above.
"""
cost = 0.0
for x, y in data:
a = self.feedforward(x)
if convert: y = vectorized_result(y)
cost += self.cost.fn(a, y)/len(data)
cost += 0.5*(lmbda/len(data))*sum(
np.linalg.norm(w)**2 for w in self.weights)
return cost
def save(self, filename):
"""Save the neural network to the file ``filename``."""
data = {"sizes": self.sizes,
"weights": [w.tolist() for w in self.weights],
"biases": [b.tolist() for b in self.biases],
"cost": str(self.cost.__name__)}
f = open(filename, "w")
json.dump(data, f)
f.close()
#### Loading a Network
def load(filename):
"""Load a neural network from the file ``filename``. Returns an
instance of Network.
"""
f = open(filename, "r")
data = json.load(f)
f.close()
cost = getattr(sys.modules[__name__], data["cost"])
net = Network(data["sizes"], cost=cost)
net.weights = [np.array(w) for w in data["weights"]]
net.biases = [np.array(b) for b in data["biases"]]
return net
#### Miscellaneous functions
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the j'th position
and zeroes elsewhere. This is used to convert a digit (0...9)
into a corresponding desired output from the neural network.
"""
e = np.zeros((10, 1))
e[j] = 1.0
return e
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))有个更加有趣的变动就是在代码中增加了 L2 规范化。尽管这是一个主要的概念上的变动,在实现中其实相当简单。对大部分情况,仅仅需要传递参数 lmbda 到不同的方法中,主要是 Network.SGD 方法。实际上的工作就是一行代码的事在 Network.update_mini_batch 的倒数第四行。这就是我们改动梯度下降规则来进行权重下降的地方。尽管改动很小,但其对结果影响却很大!
其实这种情况在神经网络中实现一些新技术的常见现象。我们花费了近千字的篇幅来讨论规范化。概念的理解非常微妙困难。但是添加到程序中的时候却如此简单。精妙复杂的技术可以通过微小的代码改动就可以实现了。
另一个微小却重要的改动是随机梯度下降方法的几个标志位的增加。这些标志位让我们可以对在代价和准确度的监控变得可能。这些标志位默认是 False 的,但是在我们例子中,已经被置为 True 来监控 Network 的性能。另外,network2.py 中的 Network.SGD 方法返回了一个四元组来表示监控的结果。我们可以这样使用:
>>> evaluation_cost, evaluation_accuracy,
... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5,
... lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True,
... monitor_evaluation_cost=True,
... monitor_training_accuracy=True,
... monitor_training_cost=True)所以,比如 evaluation_cost 将会是一个 $$30$$ 个元素的列表其中包含了每个回合在验证集合上的代价函数值。这种类型的信息在理解网络行为的过程中特别有用。比如,它可以用来画出展示网络随时间学习的状态。其实,这也是我在前面的章节中展示性能的方式。然而要注意的是如果任何标志位都没有设置的话,对应的元组中的元素就是空列表。
另一个增加项就是在 Network.save 方法中的代码,用来将 Network 对象保存在磁盘上,还有一个载回内存的函数。这两个方法都是使用 JSON 进行的,而非 Python 的 pickle 或者 cPickle 模块——这些通常是 Python 中常见的保存和装载对象的方法。使用 JSON 的原因是,假设在未来某天,我们想改变 Network 类来允许非 sigmoid 的神经元。对这个改变的实现,我们最可能是改变在 Network.__init__ 方法中定义的属性。如果我们简单地 pickle 对象,会导致 load 函数出错。使用 JSON 进行序列化可以显式地让老的 Network 仍然能够 load。
其他也还有一些微小的变动。但是那些只是 network.py 的微调。结果就是把程序从 $$74$$ 行增长到了 $$152$$ 行。
问题
- 更改上面的代码来实现 L1 规范化,使用 L1 规范化使用 $$30$$ 个隐藏元的神经网络对 MNIST 数字进行分类。你能够找到一个规范化参数使得比无规范化效果更好么?
- 看看
network.py中的Network.cost_derivative方法。这个方法是为二次代价函数写的。怎样修改可以用于交叉熵代价函数上?你能不能想到可能在交叉熵函数上遇到的问题?在network2.py中,我们已经去掉了Network.cost_derivative方法,将其集成进了CrossEntropyCost.delta方法中。请问,这样是如何解决你已经发现的问题的?
如何选择神经网络的超参数
直到现在,我们还没有解释对诸如学习率 $$\eta$$,规范化参数 $$\lambda$$ 等等超参数选择的方法。我只是给出那些效果很好的值而已。实践中,当你使用神经网络解决问题时,寻找好的超参数其实是很困难的一件事。例如,我们要解决 MNIST 问题,开始时对于选择什么样的超参数一无所知。假设,刚开始的实验中选择前面章节的参数都是运气较好。但在使用学习率 $$\eta=10.0$$ 而规范化参数 $$\lambda=1000.0$$。下面是我们的一个尝试:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 1030 / 10000
Epoch 1 training complete
Accuracy on evaluation data: 990 / 10000
Epoch 2 training complete
Accuracy on evaluation data: 1009 / 10000
...
Epoch 27 training complete
Accuracy on evaluation data: 1009 / 10000
Epoch 28 training complete
Accuracy on evaluation data: 983 / 10000
Epoch 29 training complete
Accuracy on evaluation data: 967 / 10000我们分类准确度并不比随机选择更好。网络就像随机噪声产生器一样。
你可能会说,“这好办,降低学习率和规范化参数就好了。”不幸的是,你并不先验地知道这些就是需要调整的超参数。可能真正的问题出在 $$30$$ 个隐藏元中,本身就不能很有效,不管我们如何调整其他的超参数都没有作用的?可能我们真的需要至少 $$100$$ 个隐藏神经元?或者是 $$300$$ 个隐藏神经元?或者更多层的网络?或者不同输出编码方式?可能我们的网络一直在学习,只是学习的回合还不够?可能 minibatch 的太小了?可能我们需要切换成二次代价函数?可能我们需要尝试不同的权重初始化方法?等等。很容易就在超参数的选择中迷失了方向。如果你的网络规模很大,或者使用了很多的训练数据,这种情况就很令人失望了,因为一次训练可能就要几个小时甚至几天乃至几周,最终什么都没有获得。如果这种情况一直发生,就会打击你的自信心。可能你会怀疑神经网络是不是适合你所遇到的问题?可能就应该放弃这种尝试了?
本节,我会给出一些用于设定超参数的启发式想法。目的是帮你发展出一套工作流来确保很好地设置超参数。当然,我不会覆盖超参数优化的每个方法。那是太繁重的问题,而且也不会是一个能够完全解决的问题,也不存在一种通用的关于正确策略的共同认知。总是会有一些新的技巧可以帮助你提高一点性能。但是本节的启发式想法能帮你开个好头。
宽的策略:在使用神经网络来解决新的问题时,一个挑战就是获得任何一种非寻常的学习,也就是说,达到比随机的情况更好的结果。这个实际上会很困难,尤其是遇到一种新类型的问题时。让我们看看有哪些策略可以在面临这类困难时候尝试。
假设,我们第一次遇到 MNIST 分类问题。刚开始,你很有激情,但是当第一个神经网络完全失效时,你会就得有些沮丧。此时就可以将问题简化。丢开训练和验证集合中的那些除了 $$0$$ 和 $$1$$ 的那些图像。然后试着训练一个网络来区分 $$0$$ 和 $$1$$。不仅仅问题比 $$10$$ 个分类的情况简化了,同样也会减少 80% 的训练数据,这样就给出了 $$5$$ 倍的加速。这样可以保证更快的实验,也能给予你关于如何构建好的网络更快的洞察。
你通过简化网络来加速实验进行更有意义的学习。如果你相信 $$[784, 10]$$ 的网络更可能比随机更加好的分类效果,那么就从这个网络开始实验。这会比训练一个 $$[784, 30 ,10]$$ 的网络更快,你可以进一步尝试后一个。
你可以通过提高监控的频率来在试验中获得另一个加速了。在 network2.py 中,我们在每个训练的回合的最后进行监控。每回合 $$50,000$$,在接受到网络学习状况的反馈前需要等上一会儿——在我的笔记本上训练 $$[784, 30, 10]$$ 网络基本上每回合 $$10$$ 秒。当然,$$10$$ 秒并不太长,不过你希望尝试几十种超参数就很麻烦了,如果你想再尝试更多地选择,那就相当棘手了。我们可以通过更加频繁地监控验证准确度来获得反馈,比如说在每 $$1,000$$ 次训练图像后。而且,与其使用整个 $$10,000$$ 幅图像的验证集来监控性能,我们可以使用 $$100$$ 幅图像来进行验证。真正重要的是网络看到足够多的图像来做真正的学习,获得足够优秀的估计性能。当然,我们的程序 network2.py 并没有做这样的监控。但是作为一个凑合的能够获得类似效果的方案,我们将训练数据减少到前 $$1,000$$ 幅 MNIST 训练图像。让我们尝试一下,看看结果。(为了让代码更加简单,我并没有取仅仅是 0 和 1 的图像。当然,那样也是很容易就可以实现)。
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100
Epoch 1 training complete
Accuracy on evaluation data: 10 / 100
Epoch 2 training complete
Accuracy on evaluation data: 10 / 100
...我们仍然获得完全的噪声!但是有一个进步:现在我们每一秒钟可以得到反馈,而不是之前每 10 秒钟才可以。这意味着你可以更加快速地实验其他的超参数,或者甚至近同步地进行不同参数的组合的评比。
在上面的例子中,我设置 $$\lambda=1000.0$$,跟我们之前一样。但是因为这里改变了训练样本的个数,我们必须对 $$\lambda$$ 进行调整以保证权重下降的同步性。这意味着改变 $$\lambda = 20.0$$。如果我们这样设置,则有:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 12 / 100
Epoch 1 training complete
Accuracy on evaluation data: 14 / 100
Epoch 2 training complete
Accuracy on evaluation data: 25 / 100
Epoch 3 training complete
Accuracy on evaluation data: 18 / 100
...哦也!现在有了信号了。不是非常糟糕的信号,却真是一个信号。我们可以基于这点,来改变超参数从而获得更多的提升。可能我们猜测学习率需要增加(你可以能会发现,这只是一个不大好的猜测,原因后面会讲,但是相信我)所以为了测试我们的猜测就将 $$\eta$$ 调整至 $$100.0$$:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100
Epoch 1 training complete
Accuracy on evaluation data: 10 / 100
Epoch 2 training complete
Accuracy on evaluation data: 10 / 100
Epoch 3 training complete
Accuracy on evaluation data: 10 / 100
...这并不好!告诉我们之前的猜测是错误的,问题并不是学习率太低了。所以,我们试着将 $$\eta$$ 将至 $$\eta=1.0$$:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 62 / 100
Epoch 1 training complete
Accuracy on evaluation data: 42 / 100
Epoch 2 training complete
Accuracy on evaluation data: 43 / 100
Epoch 3 training complete
Accuracy on evaluation data: 61 / 100
...这样好点了!所以我们可以继续,逐个调整每个超参数,慢慢提升性能。一旦我们找到一种提升性能的 $$\eta$$ 值,我们就可以尝试寻找好的值。然后按照一个更加复杂的网络架构进行实验,假设是一个有 $$10$$ 个隐藏元的网络。然后继续调整 $$\eta$$ 和 $$\lambda$$。接着调整成 $$20$$ 个隐藏元。然后将其他的超参数调整再调整。如此进行,在每一步使用我们 hold out 验证数据集来评价性能,使用这些度量来找到越来越好的超参数。当我们这么做的时候,一般都需要花费更多时间来发现由于超参数改变带来的影响,这样就可以一步步减少监控的频率。
所有这些作为一种宽泛的策略看起来很有前途。然而,我想要回到寻找超参数的原点。实际上,即使是上面的讨论也传达出过于乐观的观点。实际上,很容易会遇到神经网络学习不到任何知识的情况。你可能要花费若干天在调整参数上,仍然没有进展。所以我想要再重申一下在前期你应该从实验中尽可能早的获得快速反馈。直觉上看,这看起来简化问题和架构仅仅会降低你的效率。实际上,这样能够将进度加快,因为你能够更快地找到传达出有意义的信号的网络。一旦你获得这些信号,你可以尝尝通过微调超参数获得快速的性能提升。这和人生中很多情况一样——万事开头难。
好了,上面就是宽泛的策略。现在我们看看一些具体的设置超参数的推荐。我会聚焦在学习率 $$\eta$$,L2 规范化参数 $$\lambda$$,和 minibatch 大小。然而,很多的观点同样可以应用在其他的超参数的选择上,包括一些关于网络架构的、其他类型的规范化和一些本书后面遇到的如 momentum co-efficient 这样的超参数。
学习率:假设我们运行了三个不同学习率($$\eta=0.025$$、$$\eta=0.25$$、$$\eta=2.5$$)的 MNIST 网络。我们会像前面介绍的实验那样设置其他的超参数,进行 $$30$$ 回合,minibatch 大小为 $$10$$,然后 $$\lambda = 5.0$$。我们同样会使用整个 $$50,000$$ 幅训练图像。下面是一副展示了训练代价的变化情况的图:
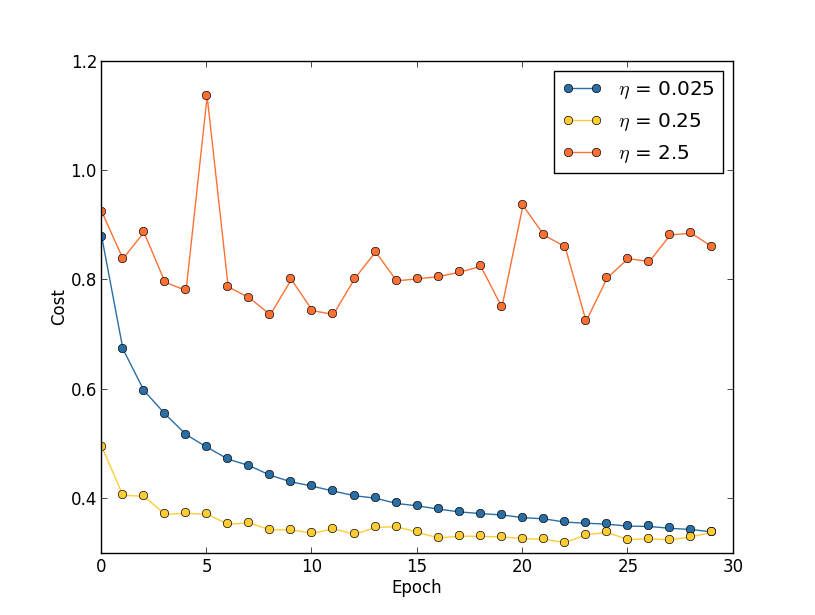
使用 $$\eta=0.025$$,代价函数平滑下降到最后的回合。使用 $$\eta=0.25$$,代价刚开始下降,在大约 $$20$$ 回合后接近饱和状态,后面就是微小的震荡和随机抖动。最终使用 $$\eta=2.5$$ 代价从始至终都震荡得非常明显。为了理解震荡的原因,回想一下随机梯度下降其实是期望我们能够逐渐地抵达代价函数的谷底的,
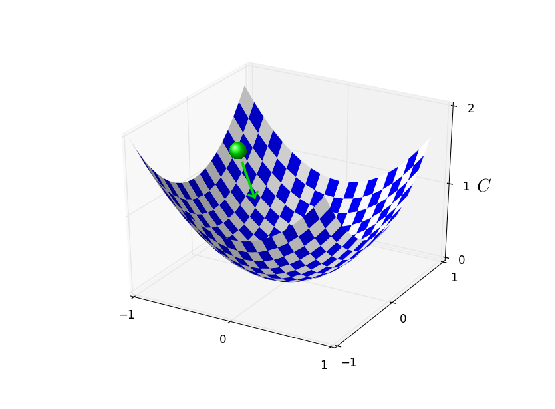
然而,如果 $$\eta$$ 太大的话,步长也会变大可能会使得算法在接近最小值时候又越过了谷底。这在 $$\eta=2.5$$ 时非常可能发生。当我们选择 $$\eta=0.25$$ 时,初始几步将我们带到了谷底附近,但一旦到达了谷底,又很容易跨越过去。而在我们选择 $$\eta=0.025$$ 时,在前 $$30$$ 回合的训练中不再受到这个情况的影响。当然,选择太小的学习率,也会带来另一个问题——随机梯度下降算法变慢了。一种更加好的策略其实是,在开始时使用 $$\eta=0.25$$,随着越来越接近谷底,就换成 $$\eta=0.025$$。这种可变学习率的方法我们后面会介绍。现在,我们就聚焦在找出一个单独的好的学习率的选择,$$\eta$$。
所以,有了这样的想法,我们可以如下设置 $$\eta$$。首先,我们选择在训练数据上的代价立即开始下降而非震荡或者增加时作为 $$\eta$$ 的阈值的估计。这个估计并不需要太过精确。你可以估计这个值的量级,比如说从 $$\eta=0.01$$ 开始。如果代价在训练的前面若干回合开始下降,你就可以逐步地尝试 $$\eta=0.1, 1.0,...$$,直到你找到一个 $$\eta$$ 的值使得在开始若干回合代价就开始震荡或者增加。相反,如果代价在 $$\eta=0.01$$ 时就开始震荡或者增加,那就尝试 $$\eta=0.001, 0.0001,...$$ 直到你找到代价在开始回合就下降的设定。按照这样的方法,我们可以掌握学习率的阈值的量级的估计。你可以选择性地优化估计,选择那些最大的 $$\eta$$,比方说 $$\eta=0.5$$ 或者 $$\eta=0.2$$(这里也不需要过于精确)。
显然,$$\eta$$ 实际值不应该比阈值大。实际上,如果 $$\eta$$ 的值重复使用很多回合的话,你更应该使用稍微小一点的值,例如,阈值的一半这样的选择。这样的选择能够允许你训练更多的回合,不会减慢学习的速度。
在 MNIST 数据中,使用这样的策略会给出一个关于学习率 $$\eta$$ 的一个量级的估计,大概是 $$0.1$$。在一些改良后,我们得到了阈值 $$\eta=0.5$$。所以,我们按照刚刚的取一半的策略就确定了学习率为 $$\eta=0.25$$。实际上,我发现使用 $$\eta=0.5$$ 在 $$30$$ 回合内表现是很好的,所以选择更低的学习率,也没有什么问题。
这看起来相当直接。然而,使用训练代价函数来选择 $$\eta$$ 看起来和我们之前提到的通过验证集来确定超参数的观点有点矛盾。实际上,我们会使用验证准确度来选择规范化超参数,minibatch 大小,和层数及隐藏元个数这些网络参数,等等。为何对学习率要用不同的方法呢?坦白地说,这些选择其实是我个人美学偏好,个人习惯罢了。原因就是其他的超参数倾向于提升最终的测试集上的分类准确度,所以将他们通过验证准确度来选择更合理一些。然而,学习率仅仅是偶然地影响最终的分类准确度的。学习率主要的目的是控制梯度下降的步长,监控训练代价是最好的检测步长过大的方法。所以,这其实就是个人的偏好。在学习的前期,如果验证准确度提升,训练代价通常都在下降。所以在实践中使用那种衡量方式并不会对判断的影响太大。
使用 Early stopping 来确定训练的回合数:正如我们在本章前面讨论的那样,Early stopping 表示在每个回合的最后,我们都要计算验证集上的分类准确度。当准确度不再提升,就终止它。这让选择回合数变得很简单。特别地,也意味着我们不再需要担心显式地掌握回合数和其他超参数的关联。而且,这个过程还是自动的。另外,Early stopping 也能够帮助我们避免过匹配。尽管在实验前期不采用 Early stopping,这样可以看到任何过匹配的信号,使用这些来选择规范化方法,但 early stopping 仍然是一件很棒的事。
我们需要再明确一下什么叫做分类准确度不再提升,这样方可实现 Early stopping。正如我们已经看到的,分类准确度在整体趋势下降的时候仍旧会抖动或者震荡。如果我们在准确度刚开始下降的时候就停止,那么肯定会错过更好的选择。一种不错的解决方案是如果分类准确度在一段时间内不再提升的时候终止。例如,我们要解决 MNIST 问题。如果分类准确度在近 $$10$$ 个回合都没有提升的时候,我们将其终止。这样不仅可以确保我们不会终止得过快,也能够使我们不要一直干等直到出现提升。
这种 $$10$$ 回合不提升就终止的规则很适合 MNIST 问题的一开始的探索。然而,网络有时候会在很长时间内于一个特定的分类准确度附近形成平缓的局面,然后才会有提升。如果你尝试获得相当好的性能,这个规则可能就会太过激进了——停止得太草率。所以,我建议在你更加深入地理解网络训练的方式时,仅仅在初始阶段使用 $$10$$ 回合不提升规则,然后逐步地选择更久的回合,比如说:$$20$$ 回合不提升就终止,$$20$$ 回合不提升就终止,以此类推。当然,这就引入了一种新的需要优化的超参数!实践中,其实比较容易设置这个超参数来获得相当好的结果。类似地,对不同于 MNIST 的问题,$$10$$ 回合不提升就终止的规则会太多激进或者太多保守,这都取决于问题的本身特质。然而,进行一些小的实验,发现好的提前终止的策略还是非常简单的。
我们还没有使用提前终止在我们的 MNIST 实验中。原因是我们已经比较了不同的学习观点。这样的比较其实比较适合使用同样的训练回合。但是,在 network2.py 中实现提前终止还是很有价值的:
问题
- 修改
network2.py来实现提前终止,并让 $$n$$ 回合不提升终止策略中的 $$n$$ 称为可以设置的参数。 - 你能够想出不同于 $$n$$ 回合不提升终止策略的其他提前终止策略么?理想中,规则应该能够获得更高的验证准确度而不需要训练太久。将你的想法实现在
network2.py中,运行这些实验和 $$10$$ 回合不提升终止策略比较对应的验证准确度和训练的回合数。
学习率调整:我们一直都将学习率设置为常量。但是,通常采用可变的学习率更加有效。在学习的前期,权重可能非常糟糕。所以最好是使用一个较大的学习率让权重变化得更快。越往后,我们可以降低学习率,这样可以作出更加精良的调整。
我们要如何设置学习率呢?其实有很多方法。一种自然的观点是使用提前终止的想法。就是保持学习率为一个常量知道验证准确度开始变差。然后按照某个量下降学习率,比如说按照 $$10$$ 或者 $$2$$。我们重复此过程若干次,知道学习率是初始值的 $$1/1024$$(或者$$1/1000$$)。那时就终止。
可变学习率可以提升性能,但是也会产生大量可能的选择。这些选择会让人头疼——你可能需要花费很多精力才能优化学习规则。对刚开始实验,我建议使用单一的常量作为学习率的选择。这会给你一个比较好的近似。后面,如果你想获得更好的性能,值得按照某种规则进行实验,根据我已经给出的资料。
A readable recent paper which demonstrates the benefits of variable learning rates in attacking MNIST isDeep, Big, Simple Neural Nets Excel on Handwritten Digit Recognition, by Dan Claudiu Cireșan, Ueli Meier, Luca Maria Gambardella, and Jürgen Schmidhuber (2010).
练习
- 更改
network2.py实现学习规则:每次验证准确度满足满足$$10$$ 回合不提升终止策略时改变学习率;当学习率降到初始值的 $$1/128$$ 时终止。
规范化参数:我建议,开始时不包含规范化($$\lambda=0.0$$),确定 $$\eta$$ 的值。使用确定出来的 $$\eta$$,我们可以使用验证数据来选择好的 $$\lambda$$。从尝试 $$\lambda=1.0$$ 开始,然后根据验证集上的性能按照因子 $$10$$增加或减少其值。一旦我已经找到一个好的量级,你可以改进 $$\lambda$$ 的值。这里搞定后,你就可以返回再重新优化 $$\eta$$。
练习
- 使用梯度下降来尝试学习好的超参数的值其实很受期待。你可以想像关于使用梯度下降来确定 $$\lambda$$ 的障碍么?你能够想象关于使用梯度下降来确定 $$\eta$$ 的障碍么?
在本书前面,我是如何选择超参数的:如果你使用本节给出的推荐策略,你会发现你自己找到的 $$\eta$$ 和 $$\lambda$$ 不总是和我给出的一致。原因自傲与,本书有一些限制,有时候会使得优化超参数变得不现实。想想我们已经做过的使用不同观点学习的对比,比如说,比较二次代价函数和交叉熵代价函数,比较权重初始化的新旧方法,使不使用规范化,等等。为了使这些比较有意义,我通常会将参数在这些方法上保持不变(或者进行合适的尺度调整)。当然,同样超参数对不同的学习观点都是最优的也没有理论保证,所以我用的那些超参数常常是折衷的选择。
相较于这样的折衷,其实我本可以尝试优化每个单一的观点的超参数选择。理论上,这可能是更好更公平的方式,因为那样的话我们可以看到每个观点的最优性能。但是,我们现在依照目前的规范进行了众多的比较,实践上,我觉得要做到需要过多的计算资源了。这也是我使用折衷方式来采用尽可能好(却不一定最优)的超参数选择。
minibatch 大小:我们应该如何设置 minibatch 的大小?为了回答这个问题,让我们先假设正在进行在线学习,也就是说使用大小为 $$1$$ 的minibatch。
一个关于在线学习的担忧是使用只有一个样本的 minibatch 会带来关于梯度的错误估计。实际上,误差并不会真的产生这个问题。原因在于单一的梯度估计不需要绝对精确。我们需要的是确保代价函数保持下降的足够精确的估计。就像你现在要去北极点,但是只有一个不大精确的(差个 $$10-20$$ 度)指南针。如果你不再频繁地检查指南针,指南针会在平均状况下给出正确的方向,所以最后你也能抵达北极点。
基于这个观点,这看起来好像我们需要使用在线学习。实际上,情况会变得更加复杂。在上一章的问题中 我指出我们可以使用矩阵技术来对所有在 minibatch 中的样本同时计算梯度更新,而不是进行循环。所以,取决于硬件和线性代数库的实现细节,这会比循环方式进行梯度更新快好多。也许是 $$50$$ 和 $$100$$ 倍的差别。
现在,看起来这对我们帮助不大。我们使用 $$100$$ 的minibatch 的学习规则如下;
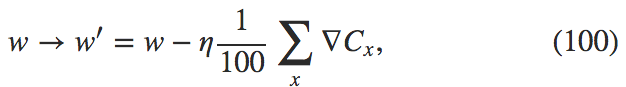
这里是对 minibatch 中所有训练样本求和。而在线学习是
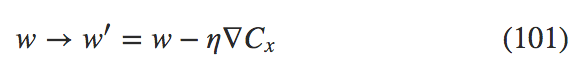
即使它仅仅是 $$50$$ 倍的时间,结果仍然比直接在线学习更好,因为我们在线学习更新得太过频繁了。假设,在 minibatch 下,我们将学习率扩大了 $$100$$ 倍,更新规则就是
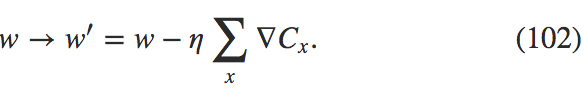
这看起来项做了 $$100$$ 次独立的在线学习。但是仅仅比在线学习花费了 $$50$$ 倍的时间。当然,其实不是同样的 100 次在线学习,因为 minibatch 中 $$\nabla C_x$$ 是都对同样的权重进行衡量的,而在线学习中是累加的学习。使用更大的 minibatch 看起来还是显著地能够进行训练加速的。
所以,选择最好的 minibatch 大小也是一种折衷。太小了,你不会用上很好的矩阵库的快速计算。太大,你是不能够足够频繁地更新权重的。你所需要的是选择一个折衷的值,可以最大化学习的速度。幸运的是,minibatch 大小的选择其实是相对独立的一个超参数(网络整体架构外的参数),所以你不需要优化那些参数来寻找好的 minibatch 大小。因此,可以选择的方式就是使用某些可以接受的值(不需要是最优的)作为其他参数的选择,然后进行不同 minibatch 大小的尝试,像上面那样调整 $$\eta$$。画出验证准确度的值随时间(非回合)变化的图,选择哪个得到最快性能的提升的 minibatch 大小。得到了 minibatch 大小,也就可以对其他的超参数进行优化了。
当然,你也发现了,我这里并没有做到这么多。实际上,我们的实现并没有使用到 minibatch 更新快速方法。就是简单使用了 minibatch 大小为 $$10$$。所以,我们其实可以通过降低 minibatch 大小来进行提速。我也没有这样做,因为我希望展示 minibatch 大于 $$1$$ 的使用,也因为我实践经验表示提升效果其实不明显。在实践中,我们大多数情况肯定是要实现更快的 minibatch 更新策略,然后花费时间精力来优化 minibatch 大小,来达到总体的速度提升。
自动技术:我已经给出很多在手动进行超参数优化时的启发式规则。手动选择当然是种理解网络行为的方法。不过,现实是,很多工作已经使用自动化过程进行。通常的技术就是网格搜索(grid search),可以系统化地对超参数的参数空间的网格进行搜索。网格搜索的成就和限制(易于实现的变体)在 James Bergstra 和 Yoshua Bengio $$2012$$ 年的论文中已经给出了综述。很多更加精细的方法也被大家提出来了。我这里不会给出介绍,但是想指出 2012 年使用贝叶斯观点自动优化超参数的论文。代码可以获得,也已经被其他的研究人员使用了。
总结:跟随上面的经验并不能帮助你的网络给出绝对最优的结果。但是很可能给你一个好的开始和一个改进的基础。特别地,我已经非常独立地讨论了超参数的选择。实践中,超参数之间存在着很多关系。你可能使用 $$\eta$$ 进行试验,发现效果不错,然后去优化 $$\lambda$$,发现这里又对 $$\eta$$ 混在一起了。在实践中,一般是来回往复进行的,最终逐步地选择到好的值。总之,启发式规则其实都是经验,不是金规玉律。你应该注意那些没有效果的尝试的信号,然后乐于尝试更多试验。特别地,这意味着需要更加细致地监控神经网络行为,特别是验证集上的准确度。
选择超参数的难度由于如何选择超参数的方法太繁多(分布在太多的研究论文,软件程序和仅仅在一些研究人员的大脑中)变得更加困难。很多很多的论文给出了(有时候矛盾的)建议。然而,还有一些特别有用的论文对这些繁杂的技术进行了梳理和总结。Yoshua Bengio 在 $$2012$$ 年的论文中给出了一些实践上关于训练神经网络用到的反向传播和梯度下降的技术的推荐策略。Bengio 对很多问题的讨论比我这里更加细致,其中还包含如何进行系统化的超参数搜索。另一篇文章是 $$1998$$ 年的 Yann LeCun、Léon Bottou、Genevieve Orr 和 Klaus-Robert Müller 的。这些论文搜集在 2012年的一本书中,这本书介绍了很多训练神经网络的常用技巧。这本书挺贵的,但很多的内容其实已经被作者共享在网络上了,也许在搜搜引擎上能够找到一些。
在你读这些文章时,特别是进行试验时,会更加清楚的是超参数优化就不是一个已经被完全解决的问题。总有一些技巧能够尝试着来提升性能。有句关于作家的谚语是:“书从来不会完结,只会被丢弃。”这点在神经网络优化上也是一样的:超参数的空间太大了,所以人们无法真的完成优化,只能将问题丢给后人。所以你的目标应是发展出一个工作流来确保自己快速地进行参数优化,这样可以留有足够的灵活性空间来尝试对重要的参数进行更加细节的优化。
设定超参数的挑战让一些人抱怨神经网络相比较其他的机器学习算法需要大量的工作进行参数选择。我也听到很多不同的版本:“的确,参数完美的神经网络可能会在这问题上获得最优的性能。但是,我可以尝试一下随机森林(或者 SVM 或者……这里脑补自己偏爱的技术)也能够工作的。我没有时间搞清楚那个最好的神经网络。” 当然,从一个实践者角度,肯定是应用更加容易的技术。这在你刚开始处理某个问题时尤其如此,因为那时候,你都不确定一个机器学习算法能够解决那个问题。但是,如果获得最优的性能是最重要的目标的话,你就可能需要尝试更加复杂精妙的知识的方法了。如果机器学习总是简单的话那是太好不过了,但也没有一个应当的理由说机器学习非得这么简单。
其他技术
本章中讲述的每个技术都是很值得学习的,但是不仅仅是由于那些我提到的愿意。更重要的其实是让你自己熟悉在神经网络中出现的问题以及解决这些问题所进行分析的方式。所以,我们现在已经学习了如何思考神经网络。本章后面部分,我会简要地介绍一系列其他技术。这些介绍相比之前会更加粗浅,不过也会传达出关于神经网络中多样化的技术的精神。
随机梯度下降的变种
通过反向传播进行的随机梯度下降已经在 MNIST 数字分类问题上有了很好的表现。然而,还有很多其他的观点来优化代价函数,有时候,这些方法能够带来比 minibatch 随机梯度下降更好的效果。本节,我会介绍两种观点,Hessian 和 momentum 技术。
Hessian 技术:为了更好地讨论这个技术,我们先把神经网络放在一边。相反,我直接思考最小化代价函数 $$C$$ 的抽象问题,其中 $$C$$ 是多个参数的函数,$$w=w_1,w_2,...$$,所以 $$C=C(w)$$。借助于泰勒展开式,代价函数可以在点 $$w$$ 处被近似为:
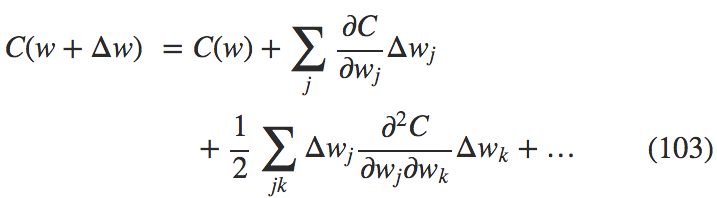
我们可以将其压缩为:
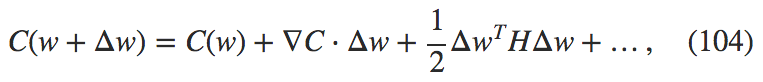
其中 $$\nabla C$$ 是通常的梯度向量,$$H$$ 就是矩阵形式的 Hessian 矩阵,其中 $$jk$$-th 项就是 $$\partial^2 C/\partial w_j\partial w_k$$。假设我们通过丢弃更高阶的项来近似 $$C$$,

使用微积分,我们可证明右式表达式可以进行最小化,选择:

根据(105)是代价函数的比较好的近似表达式,我们期望从点 $$w$$ 移动到 $$w+\Delta w = w - H^{-1}\nabla C$$ 可以显著地降低代价函数的值。这就给出了一种优化代价函数的可能的算法:
- 选择开始点,$$w$$
- 更新 $$w$$ 到新点 $$w' = w - H_{-1}\nabla C$$,其中 Hessian $$H$$ 和 $$\nabla C$$ 在 $$w$$ 处计算出来的
- 更新 $$w'$$ 到新点 $$w'' = w' - H'^{-1}\nabla' C$$,其中 Hessian $$H'$$ 和 $$\nabla' C$$ 在 $$w'$$ 处计算出来的
- ...
实际应用中,(105)是唯一的近似,并且选择更小的步长会更好。我们通过重复地使用改变量 $$\Delta w = -\eta H^{-1} \nabla C$$ 来 改变 $$w$$,其中 $$\eta$$ 就是学习率。
这个最小化代价函数的方法常常被称为 Hessian 技术 或者 Hessian 优化。在理论上和实践中的结果都表明 Hessian 方法比标准的梯度下降方法收敛速度更快。特别地,通过引入代价函数的二阶变化信息,可以让 Hessian 方法避免在梯度下降中常碰到的多路径(pathologies)问题。而且,反向传播算法的有些版本也可以用于计算 Hessian。
如果 Hessian 优化这么厉害,为何我们这里不使用它呢?不幸的是,尽管 Hessian 优化有很多可取的特性,它其实还有一个不好的地方:在实践中很难应用。这个问题的部分原因在于 Hessian 矩阵的太大了。假设你有一个 $$10^7$$ 个权重和偏差的网络。那么对应的 Hessian 矩阵会有 $$10^7 \times 10^7=10^14$$ 个元素。这真的是太大了!所以在实践中,计算 $$H^{-1}\nabla C$$ 就极其困难。不过,这并不表示学习理解它没有用了。实际上,有很多受到 Hessian 优化启发的梯度下降的变种,能避免产生太大矩阵的问题。让我们看看其中一个称为基于 momentum 梯度下降的方法。
