打散算法的三种解决方案及其选型场景

背景

打散是在推荐、广告、搜索系统的结果基础上，提升用户视觉体验的一种处理。主要方法是对结果进行一个呈现顺序上的重排序，令相似品类的对象分散开，避免用户疲劳。 算法端传出的推荐结果，往往具有以下几个痛点： 1、相似品类的商品易扎堆。显然的，如果商品的各特征相似，其获得的推荐分数也容易相近，而满目的同款肯定不是用户期望的结果。 2、对用户的偏好捕捉太强。用户心理层面，对于隐私或者偏好被完美捕捉这件事是敏感的，过于精准的结果不但容易导致用户的反感，也容易限制用户潜力的转化。 3、产生的错误容易被放大。对于几乎没有什么使用痕迹的用户，很容易出现对仅有特征的放大，从而就容易产生错误推荐。 而打散算法，通过呈现顺序的改变，将相似品类分开，缓冲了推荐系统和用户的交互，提升了用户体验，是算法赋能落地的最后一步。

问题定义

首先，我们明确打散算法的定义。其输入是算法端根据用户偏好程度排列的有序列表，每个对象拥有一个或多个需要加以区分的属性，输出的要求是将相似属性分散开后的一个列表。 其中会涉及到这几个细节： 1、打散程度。究竟是让相同类目的尽可能分隔开，还是只要间隔一定距离就可以满足要求？ 2、打散依据的维度。是按照一种属性分开就可以，还是存在多种需要考虑分开的因素？ 3、打散的性能。作为经常调用的一种接口，性能的优化当然是越多越好 值得注意的是，我们并不希望丢失算法端系统带来的用户个性因素，所以如何在打散的基础上，充分利用好原对象的顺序，也是非常值得权衡的问题。

解决方案

从三个不同的维度，我们将讨论三种比较通用的打散办法。 三种方法中，打散程度最彻底的，是按列打散法；能综合多维度考虑的，是权重分配法；只需要局部计算来提高性能的，是滑动窗口法。

1）按列打散法

既然要避免相似属性的内容在呈现时相邻，很直接的思路是我们将不同属性的装在不同的桶里，每次要拿的时候尽量选择不同的桶。这样就可以实现将元素尽量打散。 如下图所示，在这个例子中，初始的列表是共有三类（蓝、黄、红）：

将他们按序装到桶里（通常是HashMap）：

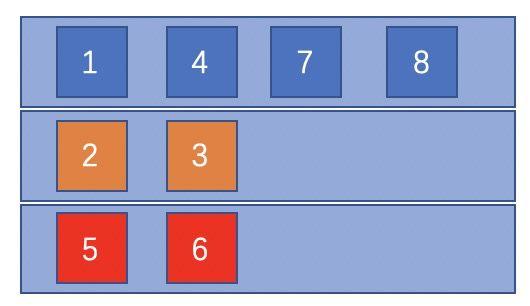
这个时候，我们把每个桶按列取出元素，即可以保证元素被最大程度打散，最终结果为

为了保证对原算法结果的保留，我们在取每一列时都有一次按原序排序的过程。 这种算法的优点为： 1、简单直接，容易实现 2、打散效果好，虽然排序可能导致元素在列的开头和结尾偶然相邻，但是在末尾之前，最多相邻元素为2，不影响体验 3、性能比较稳定，不易受输入结构影响 缺点为： 1、末尾打散失效，容易出现扎堆 2、对原序的尊重性不算强，即使有推荐系数非常低的对象也强制出现在前面 3、只能考虑一种维度的分类，无法综合考虑别的因素 同时也可以看出，这个算法对类目数量有着相当的依赖，如果类目足够细致，这个算法的缺点就可以被部分掩盖，性能上，时间和空间消耗都是O(n)的

2）权重分配法

当我们想综合考虑多个因素时，无法很直观的将每个商品直接分类，这个时候可以采用权重分配法。 首先，我们对每个对象定义一个新的权重：

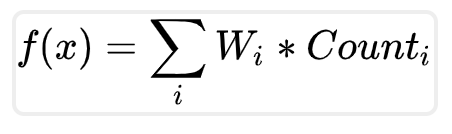
其中，W为人为为每个属性分配的系数，代表着打散的优先度，而Count则代表着该对象在此属性的表现（相同属性已经出现了多少次）。直观的来说，相似属性已经出现了越多次，权重值就会越大，并且在函数计算过程中，天然考虑了原本顺序的因素，所以计算出权重后，无须其他处理，只需要按权重排序即可。 以下图为例，如果我们规定字体颜色权重系数为2，色块颜色权重系数为1 那么，在1、2号，他们的字体颜色和色块都没出现过，则权重为0，到3号时，都出现过1次，则权重为 2 * 1 + 1 * 1 = 3，以此类推，8号时，其字体颜色出现过2次，色块颜色出现过3次，则权重为 2 * 2 + 1 * 3 = 7

这样，只需要采用一个排序操作，即可根据权重进行打散处理。

可以看出，通过设置更重的权重系数，我们实现了优先打乱了字体颜色，色块信息因为系数较低，可以容忍他们有限度的相邻。 这种算法的优点为： 1、实现同样简单直接 2、综合考虑了不同因素的打散，可以通过调整权重系数，轻易调整对打散的倾向程度 3、通过对权重计算函数的修改，可以很轻松的融入别的考量，如想更尊重原排序，也可以将原序加入权重计算 缺点为： 1、因为权重计算的累积效应，本算法仍然容易末尾失效 2、最后对整体排序，性能为O(n logn)，相对有优化空间

3）窗口滑动法

以上两种，都是在我们彻底考虑全局后产生的算法，复杂度计算中n的变量也是整个原序列大小，但是，实际场景中，用户并不会一下看到整个序列，往往一次返回topN个，填满用户窗口就可以了。 这个时候，我们应当发掘一种只参考局部的方法，基本思想就是滑动窗口。 如下图所示，我们开启一个size为3的窗口，以此来类比用户的接收窗口，规定窗口内不能有元素重复，即模拟用户看到的一个展示页面没有重复，如果窗口内发现重复元素，则往后探测一个合适的元素与当前元素交换。 在第一步时，我们探测到2、3同类，于是将3拿出来，往后探测到4符合3处的要求，于是交换3、4，窗口往后滑动一格。 第二步时，发现还存在窗口中2、3同类，再将3、5交换，窗口往后滑动一格，发现窗口内无冲突，再滑动一格。 第三步时，发现5、6同类，将6、7交换，窗口滑动到最后，尽管还发现了7、8同类，但彼时已无可交换元素，便不作处理。

这种算法的优点为只需要局部计算，不需要完全打散，适应了topN的需求；而缺点也同样明显，其健壮性不佳，受序列分布的影响很大，同样也避免不了末尾堆积的缺陷。

综合考量

根据前文的讨论，我们对这几种方法有如下的结论：

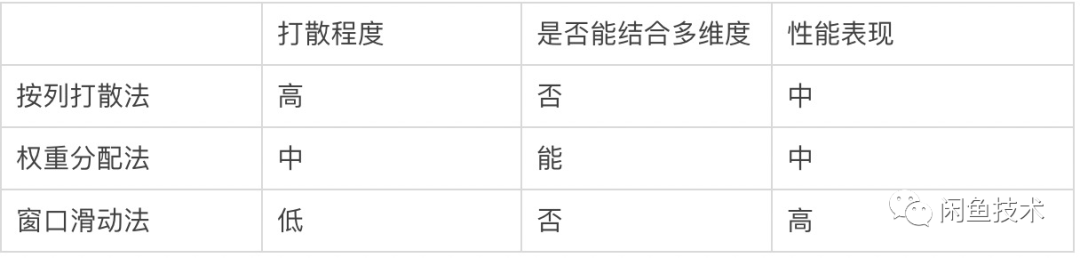
其中，为了便于直观的比较三种方法的性能表现，我们生成了完全随机的十万条数据，在笔记本环境下测试了在不同规模下三种算法的表现。其中横坐标表示输出数据的规模，纵坐标表示运行的时间（单位:ms）

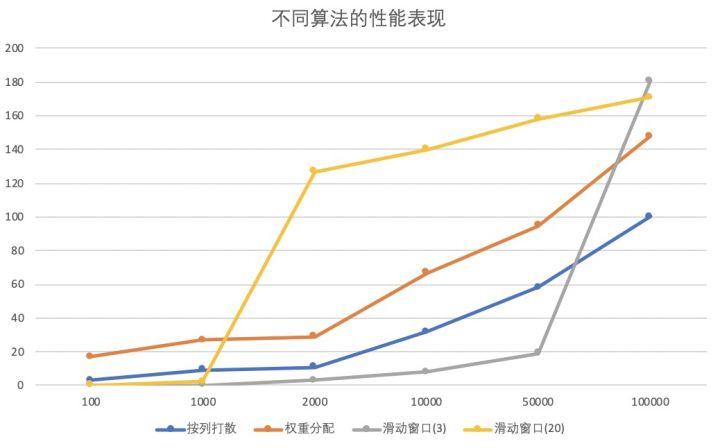
可以看出，在一定数据范围内，滑动窗口法拥有极大的优势，但是性能与窗口大小也有极大关系，如果窗口范围过大，冲突就多，交换速度会极大下滑。

综合来说，三种算法的适用场景如下：

• 如果平常使用的场景，单一维度打散的话，采用按列打散是完全可以的
• 如果追求性能且原排列分布已经较为稀疏了，选择小单位的滑动窗口更佳
• 如果要引入多维度，则权重分配法就必不可少了

本文提出的所有算法性能都在O(n)、O(nlogn)的级别上，而且因为实际场景往往规模极小，所以并不会成为应用中的性能瓶颈，也为修改和权衡留下了很大的空间。之后，可以在全局与局部的调和、末尾堆积等方面，对这个问题更进一步讨论。

选用实例