详解 SQL 关联子查询。

在背景介绍中我们将讲讲常见的关联子查询的语义，关联子查询语法的好处以及其执行时对数据库系统的挑战。第二章中我们将主要介绍如何将关联子查询改写为普通的查询的形式，也就是解关联。第三章中我们会介绍解关联中的优化方法。

一 背景介绍

关联子查询是指和外部查询有关联的子查询，具体来说就是在这个子查询里使用了外部查询包含的列。

因为这种可以使用关联列的灵活性，将sql查询写成子查询的形式往往可以极大的简化sql以及使得sql查询的语义更加方便理解。下面我们通过使用tpch schema来举几个例子以说明这一点。tpch schema是一个典型的订单系统的database，包含customer表，orders表，lineitem表等，如下图：

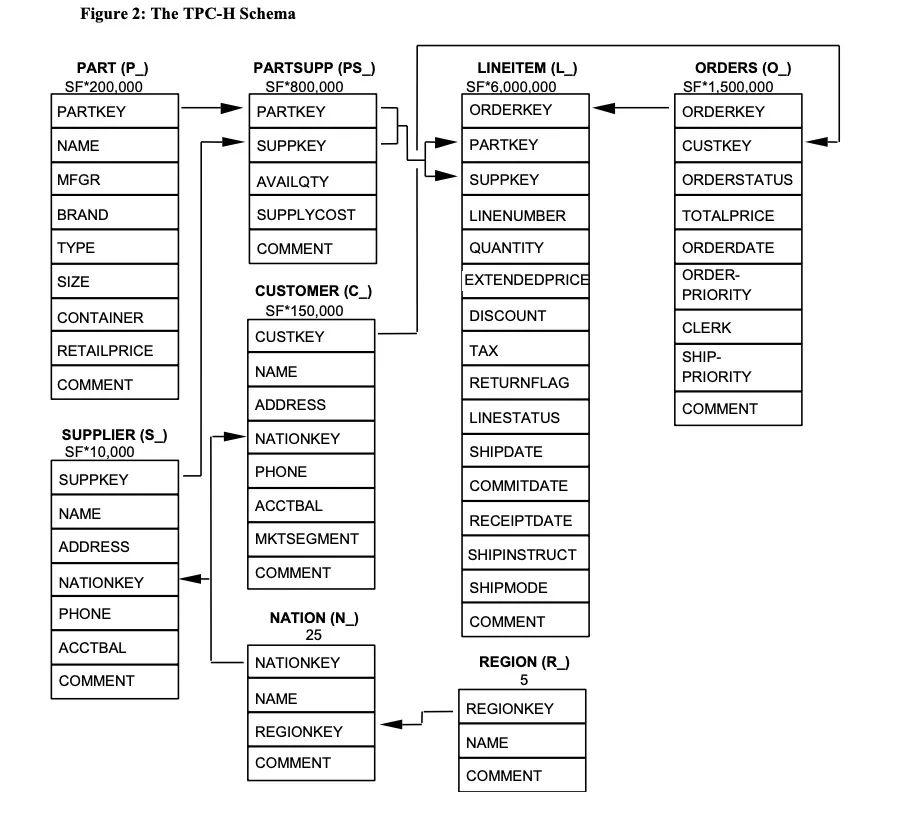
假如我们希望查询出“所有从来没有下过单的客户的信息”，那么我们可以将关联子查询作为过滤条件。使用关联子查询写出的sql如下。可以看到这里的not exists子查询使用列外部的列c_custkey。

-- 所有从来没有下过单的客户的信息
select c_custkey
from
  customer
where
  not exists (
    select
      *
    from
      orders
    where
      o_custkey = c_custkey
  )

如果不写成上面的形式，我们则需要考虑将customer和orders两个表先进行left join，然后再过滤掉没有join上的行，同时我们还需要markorder的每一行，使得本来就是null的那些。查询sql如下：

-- 所有从来没有下过单的客户的信息
select c_custkey
from
  customer
  left join (
    select
      distinct o_custkey
    from
      orders
  ) on o_custkey = c_custkey
where
  o_custkey is null

从这个简单的例子中就可以看到使用关联子查询降低了sql编写的难度，同时提高了可读性。

除了在exists/in子查询中使用关联列，关联子查询还可以出现在where中作为过滤条件需要的值。比如tpch q17中使用子查询求出一个聚合值作为过滤条件。

-- tpch q17
SELECT Sum(l1.extendedprice) / 7.0 AS avg_yearly 
FROM   lineitem l1, 
       part p
WHERE  p.partkey = l1.partkey 
       AND p.brand = 'Brand#44' 
       AND p.container = 'WRAP PKG' 
       AND l1.quantity < (SELECT 0.2 * Avg(l2.quantity) 
                         FROM   lineitem l2
                         WHERE  l2.partkey = p.partkey);

除了出现在where里面，关联子查询可以出现在任何允许出现单行(scalar)的地方，比如select列表里。如果我们需要做报表汇总一些customer的信息，希望对每一个customer查询他们的订单总额，我们可以使用下面包含关联子查询的sql。

-- 客户以及对应的消费总额
select
  c_custkey,
  (
    select sum(o_totalprice)
    from
      orders
    where o_custkey = c_custkey 
    ）
from
  customer

更复杂一些的比如，我们希望查询每一个customer及其对应的在某个日期前已经签收的订单总额。利用关联子查询只需要做一些小的改变如下：

select
  c_custkey,
  (
    select
      sum(o_totalprice)
    from
      orders
    where
      o_custkey = c_custkey
      and '2020-05-27' > (
        select
          max(l_receiptdate)
        from
          lineitem
        where
          l_orderkey = o_orderkey
      ) 
    ）
from
   customer

看了这些例子，相信大家都已经感受到使用关联子查询带来的便捷。但是同时关联子查询也带来了执行上的挑战。为了计算关联结果的值（子查询的输出），需要iterative的执行方式。

以之前讨论过的tpch 17为例子：

SELECT Sum(l1.extendedprice) / 7.0 AS avg_yearly 
FROM   lineitem l1, 
       part p
WHERE  p.partkey = l1.partkey 
       AND p.brand = 'Brand#44' 
       AND p.container = 'WRAP PKG' 
       AND l1.quantity < (SELECT 0.2 * Avg(l2.quantity) 
                         FROM   lineitem l2
                         WHERE  l2.partkey = p.partkey);

这里的子查询部分使用了外部查询的列 p.partkey。

SELECT 0.2 * Avg(l2.quantity) 
FROM   lineitem l2
WHERE  l2.partkey = p.partkey  -- p.partkey是外部查询的列

优化器将这个查询表示为如下图的逻辑树：

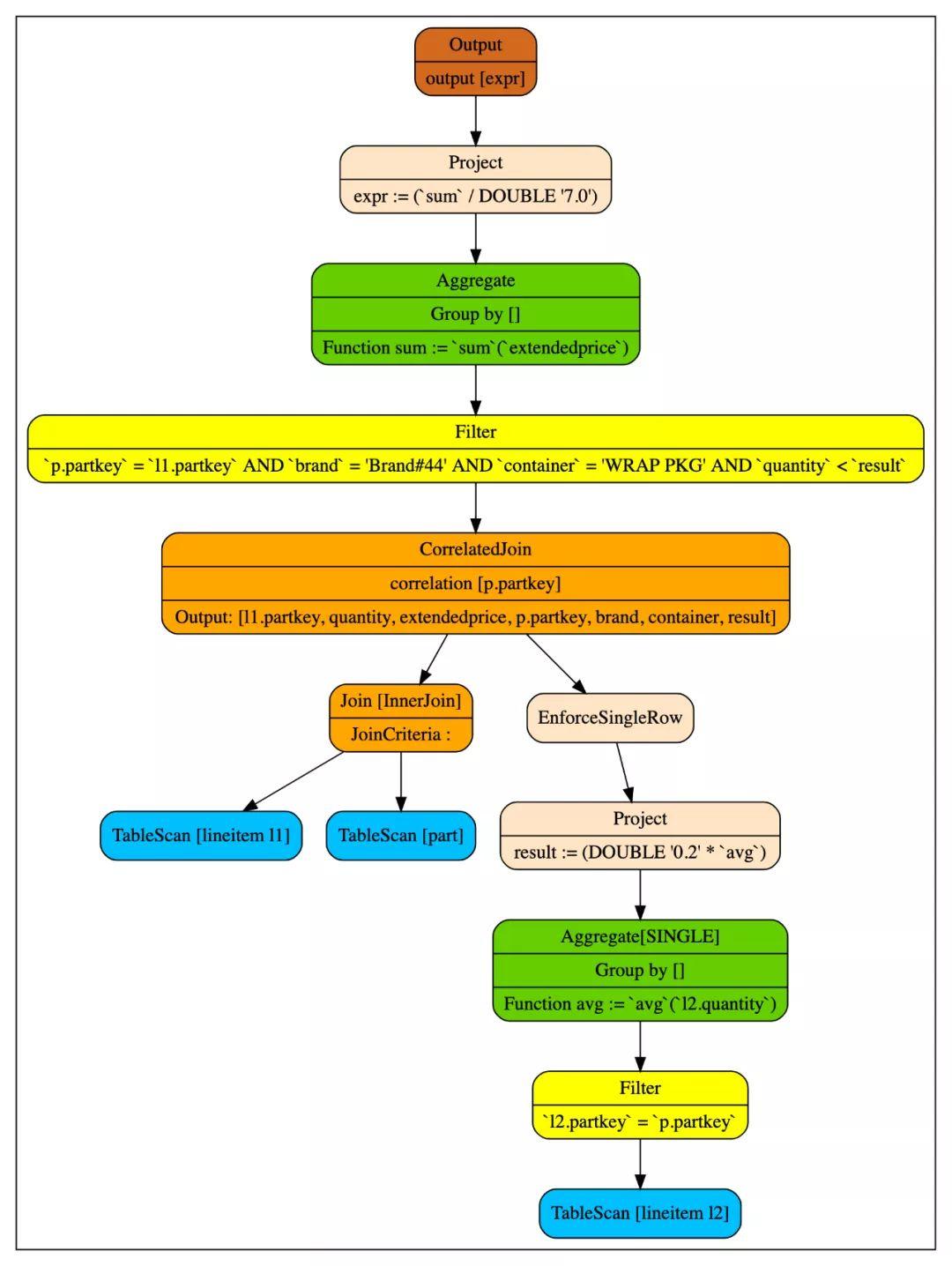
如果数据库系统不支持查看逻辑树，可以通过explain命令查看物理计划，一般输出如下图：

+---------------+
| Plan Details  |
+---------------+
 1- Output[avg_yearly] avg_yearly := expr
 2    -> Project[] expr := (`sum` / DOUBLE '7.0')
 3        - Aggregate sum := `sum`(`extendedprice`)
 4            -> Filter[p.`partkey` = l1.`partkey` AND `brand` = 'Brand#51' AND `container` = 'WRAP PACK' AND `quantity` < `result`]
 5                - CorrelatedJoin[[p.`partkey`]]
 6                    - CrossJoin
 7                        - TableScan[tpch:lineitem l1]
 8                        - TableScan[tpch:part p]
 9                    - Scalar
10                        -> Project[] result := (DOUBLE '0.2' * `avg`)
11                            - Aggregate avg := `avg`(`quantity`)
12                                -> Filter[(p.`partkey` = l2`partkey`)] 
13                                    - TableScan[tpch:lineitem l2]

我们将这个连接外部查询和子查询的算子叫做CorrelatedJoin(也被称之为lateral join, dependent join等等。它的左子树我们称之为外部查询(input)，右子树称之为子查询(subquery)。子查询中出现的外部的列叫做关联列。在栗子中关联列为p.partkey。

例子中对应的逻辑计划和相关定义如下图所示，explain返回结果中第6-8行为外部查询，9-13行为子查询，关联部位在子查询中第12行的filter。

这个算子的输出等价于一种iterative的执行的结果。也就将左子树的每一行关联列的值带入到右子树中进行计算并返回一行结果。有些类似将子查询看成一个user defined function（udf），外部查询的关联列的值作为这个udf的输入参数。需要注意的是，我们需要子查询是确定的，也就是对同样值的关联列，每次运行子查询返回的结果应该是确定的。

在上图的栗子中，如果外部查询有一行的p.partkey的值为25，那么这一行对应的correlatedjoin的输出就是下面这个查询的结果：

-- p.partkey = 25 时对应的子查询为
SELECT 0.2 * Avg(l2.quantity) 
FROM   lineitem l2
WHERE  l2.partkey = 25

需要注意的是，如果计算结果为空集，则返回一行null。而如果运行中子查询返回了超过一行的结果，应该报运行时错误。在逻辑计划里，用enforcesinglerow这个node来约束。

从上面的介绍中可以发现，CorrelatedJoin这个算子打破了以往对逻辑树自上而下的执行模式。普通的逻辑树都是从叶子节点往根结点执行的，但是CorreltedJoin的右子树会被带入左子树的行的值反复的执行。

correlatedjoinnode的输出就是在外部查询的结果上增加了一列，但是可以看到这种iterative的执行方式的复杂度和将外部查询和子查询关联产生之前的那部分树进行cross join的复杂度相同。

同时，这样iterative的执行方式对分布式数据库系统来说是很大的挑战。因为需要修改执行时调度的逻辑。而且我们可以看到，这样的执行方式如果不进行结果的缓存，会进行很多重复结果的计算。

传统的优化器的优化规则没有特别的针对Correlatedjoin node进行处理，为了支持关联子查询的这种iterative的形式，在优化器初始阶段就会把Correlatedjoin进行等价转换，转换过后的逻辑树用join，aggregation等普通算子来进行关联子查询结果的计算。这个过程被称为解关联（decorrelation/unnesting）。下面一章我们主要介绍常见的解关联的方式。

二 常见的解关联方式

为了方便起见，我们在这一章只讨论scalar关联子查询，就是会输出一列值的关联子查询。

在讨论如何解关联之前，我们总结一下关联子查询的输出有以下特点：

• correlated join算子的计算结果为在外部查询上增加一列。
• 增加的那一列的结果为将外部查询关联列的值带入子查询计算得出的。当计算结果超过一行则报错，计算结果为空则补充null。
• 不同于join算子，correlated join不改变外部查询的其他列（不少行也不膨胀）。

解开关联的关键在于使得子查询获得对应的外部查询的行的值。

表现在计划上，就是将correleted join算子向右下推到产生关联的部位的下面。当correlated join算子的左右子树没有关联列的时候，correlated join算子就可以转换成join算子。这样子查询就通过和外部查询join的方式获得了关联列的值，从而可以自上而下计算，回到原本的计算方式。如下图，下图中rest subquery为在关联产生部位之前的子查询部分。当correlated join 推到产生关联的部位之下，就可以转换为普通的join了。

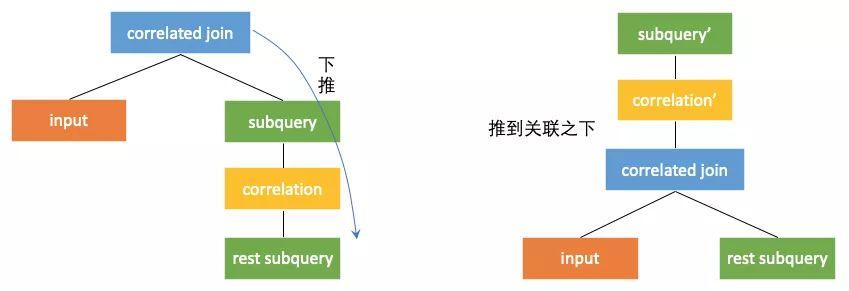
correlated join推过的那些算子都是需要进行改写，以保持等价性（上图的栗子中subquery变为了subquery’）。

1 下推规则

论文Orthogonal Optimization of Subqueries and Aggregation[2]给出了将correlatedjoin算子下推到其他算子（filter，project，aggregation，union 等）下面的的等价转换规则。但是文中的correlatedjoin算子是会过滤外部查询的行数的，类似于inner join（论文中称为 ）。我们这里讨论更加general的类似于left join的 correlatedjoin (论文中称为 )，并讨论如果要保证外部查询行数不被过滤需要做哪些改写。

由于篇幅限制，下面我们只介绍下推到filter，project，aggregation算子下面的等价规则。

为了简单起见，我们在逻辑树中去掉了enforcesinglerow。

转换1 无关联时转换为join

回顾前文所说，correlated join算子的左子树为input，右子树为subquery。当correlated join的左右子树没有关联的时候，这个时候对外部查询的每一行，子查询的结果都是相同的。

我们就可以把correlated join转换成普通的没有join criteria的leftjoin算子。

注：需要在subquery上添加enforcesinglerow来保证join语义和correlatedjoin相同（不会造成input的膨胀）。

转换2 简单关联条件时转换为join

当correlated join右子树中最上面的节点为一个关联filter而他的下面无关联时，可以直接将这个filter放到left join的条件中，也可以理解为filter上提。如下图：

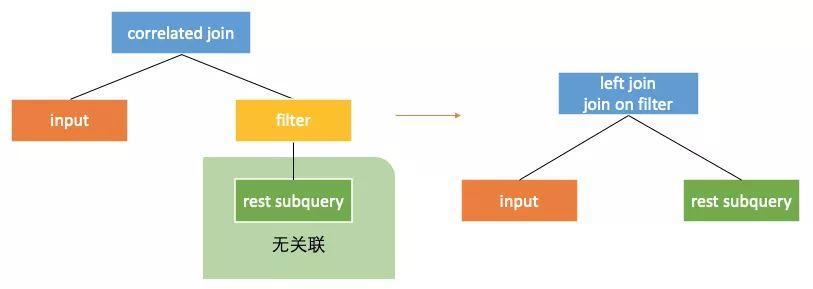
转换3 下推穿过filter

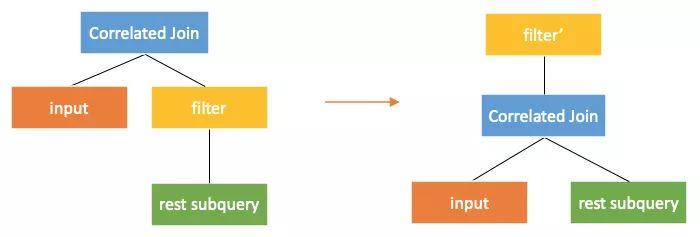
论文中correlatedjoin*可以直接推过filter。如果需要下推的为correlatedjoin，则需要对filter进行改写，改写成带有case when的project。当subquery的行不满足filter的条件时应输出null。

转换4 下推穿过project

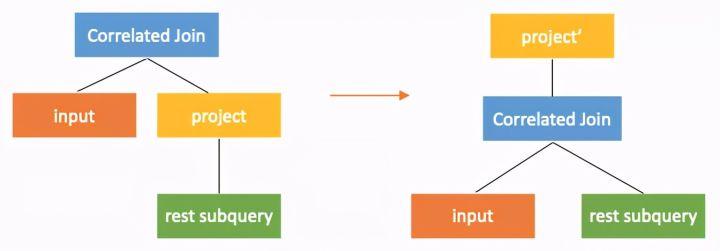
correlated join下推过project，需要在project中添加input的输出列。

转换5 下推穿过aggregation

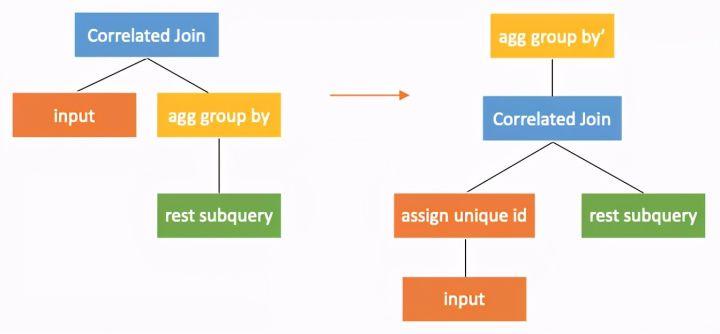
correlated join下推到带有group by的aggregation时，需要对aggregation进行改写。

改写为在aggregation的group by的列中增加外部查询的全部列。这里要求外部查询一定有key，如果没有则需要生成临时的key。生成可以的算子在图中为assignuniqueid算子。

如果aggregation为全局的，那么还需要进行额外的处理。如下图：

correlated join下推到全局aggregation的时候，需要对aggregation增加input的列(以及key)作为group by的列。这个下推规则还需要一个前提，那就是aggregation函数需要满足满足特性 agg(Ø)=agg(null) 。这个的意思就是aggragtion函数需要对空集和对null的计算结果是相同的。

注：在mysql和AnalyticDB for MySQL（阿里云自研的云原生数据仓库[1]，兼容mysql语法，下文简称ADB）的语法里，sum, avg等都不满足这个特性。空集的平均值为0, 而对包含null值的任意集合取平均值结果为null不为0。所以需要mark子查询里的每一行，对空集进行特别的处理，在这里就不展开解释了。

论文Orthogonal Optimization of Subqueries and Aggregation[2]反复运用上面这些规则进行correlatedjoin的下推，直到correlatedjoin可以转换为普通的join。

带入之前的tpch q17的栗子中，我们先使用将correlated join推到子查询中的project下面，查询变为：

然后下推穿过这个agg，并改写这个agg，如下图：

这里我们忽略 avg(Ø)!=avg(null) 。如果考虑这个情况，则需要mark子查询全部的行，在correlated join之后根据子查询的结果结合mark的值对空集进行特别处理（将mark了的行的值从null变为0）。感兴趣的读者可以参考下一张中q17的最终计划。

接着直接调用之前的规则2，上提这个filter。这样这个查询就变为普通的没有关联的查询了。

2 结果复用

回顾上一节所说，子查询的查询结果是带入每一行关联列的值之后计算得出的，那么显而易见相同值的关联列带入子查询中计算出的结果是完全相同的。在上面的栗子中，对同样的p.partkey，correlatedjoin输出的子查询的结果是相等的。如下图中外部查询partkey为25的话产生的关联子查询时是完全相同的，那么结果也自然相同。

15年Newmann的论文Unnesting Arbitrary Queries[3]介绍了一种方法就是先对外部查询里关联列取distinct，再将correlated join返回的值和原本的外部查询根据关联列进行left join，如下图所示：

这里的not distinct join的条件对应mysql里面的<=>，null<=>null的结果为true，是可以join到一起的。

带入到之前的例子中如下图所示，对外部查询的关联列partkey先进行distinct，然后带入子查询计算结果，最后再通过join将对应的结果接到原本的外部查询上。

如果进行了上述转换，那么我们可以认为新的input的关联列永远是distinct的。而现在的correlatedjoin*算子可以允许input的列被过滤。这样做的好处除了对于相同的列不进行重复的子查询的计算之外，主要还有下面两个：

• 新的外部查询是永远有key的，因为distinct过了。
• correlatedjoin*算子由于过滤外部查询的列，所以它的下推更为简单（不需要assignuniqueid，不需要保留全部行）。

进行上述的转换后，紧接着再套用之前的等价下推规则，我们又可以将correlatedjoin*下推到一个左右子树没有关联的地方，从而改写为inner join。

如果按照Unnesting Arbitrary Queries[3]的方法进行解关联，需要将input的一部分结果进行复用，这个复用需要执行引擎的支持。需要注意的是，当系统不支持复用的时候，我们需要执行两次input的子树（如下图），这个时候就需要input这颗子树的结果是deterministic的，否则无法用这个方法进行解关联。

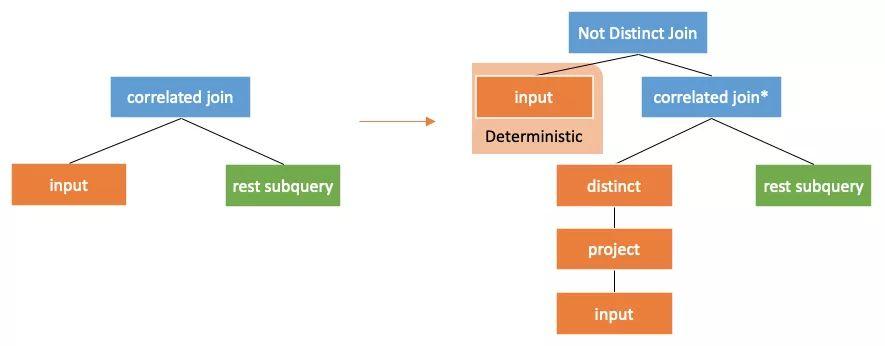
三 关联子查询的优化

在ADB的优化器中，逻辑计划会根据每一条转换规则进行匹配和转换，也就意味着在关联解开之后不需要关心解关联产生的计划的效率而将它直接交给后续的优化规则。但是现实并不是那么的美好，因为后续规则不够完备，以及解关联之后丢失了外部查询和子查询之间的关系，我们希望在解关联的时候就将计划尽可能优化。

1 exists/in/filter关联子查询

在之前的章节中为了简化，我们只讨论了scalar子查询。因为exists/in这些子查询都可以改写成scalar子查询。比如将exists改写为count(*) > 0

但是可以看到，如果子查询的返回结果被用来过滤外部查询的行，实际上会简化整个解关联的过程。所以我们对exists/in这样的子查询进行特殊处理，在语法解析时就进行区分。在解关联的过程中，如果可以使用semijoin/antijoin算子进行解关联则直接解开关联，否则后续会转化成scalar子查询也就是correlatedjoin的形式。

2 关联条件的上提

看到这里会发现，随着correlatedjoin的下推，这个逻辑树会变得更加复杂，所以我们在下推之前会在子查询内部进行关联算子的上提。当这个逻辑就是产生关联的算子越高，correlatedjoin就可以早点推到关联部位的下面。比如下面这个查询：

SELECT t1.c2
FROM
  t1
WHERE t1.c2 < (
    SELECT 0.2 * max(t2.x)
    FROM
      t2
    WHERE t2.c1 = t2.c1
    GROUP BY t2.c1
  );

这里由于t2.c1 = t2.c1可以推到agg 上面(因为对于子查询这是一个在group by列上的条件)，我们就可以进行下面的转换。先把关联的filter上提（有时需要改写），这样就只要把correlatedjoin推过filter，调用转换2就可以了。

更具体的例子就是前文提到的tpch q17。这里的scalar子查询作用在过滤条件中的情况也可以进行进一步改写。

下图为按照之前说的理论下推correlated join并改写为left join之后的逻辑计划。

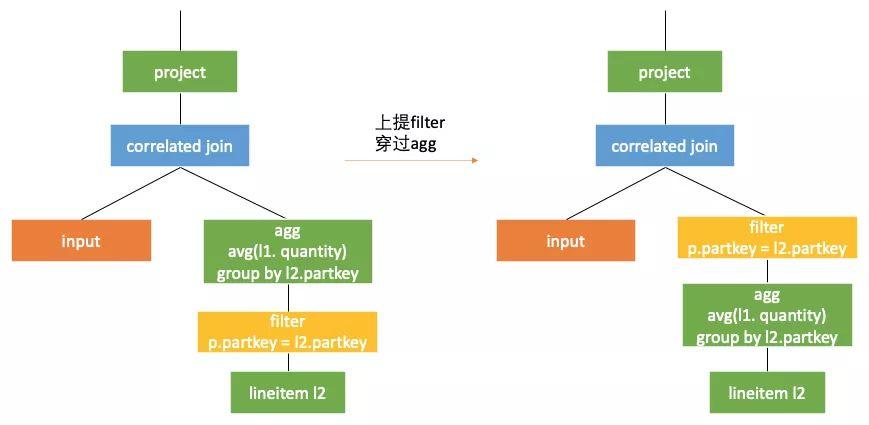
而由于这个scalar子查询是作为filter条件的，这种情况下子查询没有结果返回为null对应的外部查询是一定会被过滤掉的。所以correlatedjoin可以直接转为 correlatedjoin*，再加上将filter进行上提，我们可以得到下面的计划。这样改写的好处是可以在join前先进行agg(early agg)。坏处就是如果不小心处理，很容易造成语义不等价造成count bug。

3 代价相关的子查询优化

利用window算子解关联

回顾到目前为止我们讲的这些，是不是印象最深刻的在于correlatedjoin算子是在外部查询上增加一列。而他的这个行为和window算子类似。window算子的语义就是不改变输入的行数，只是在每一行上增加一个在window的frame里计算出的值。所以我们可以利用window算子进行解关联，如果感兴趣可以参考这两篇论文Enhanced Subquery Optimizations in Oracle[4]和 WinMagic : Subquery Elimination Using Window Aggregation[5]。

window解关联的改写就是在外部查询包含子查询中全部的表和条件时，可以直接使用window将子查询的结果拼接到外部查询上。他好处是节约了很多tablescan。比如说tpch q2。可以进行下面的改写：

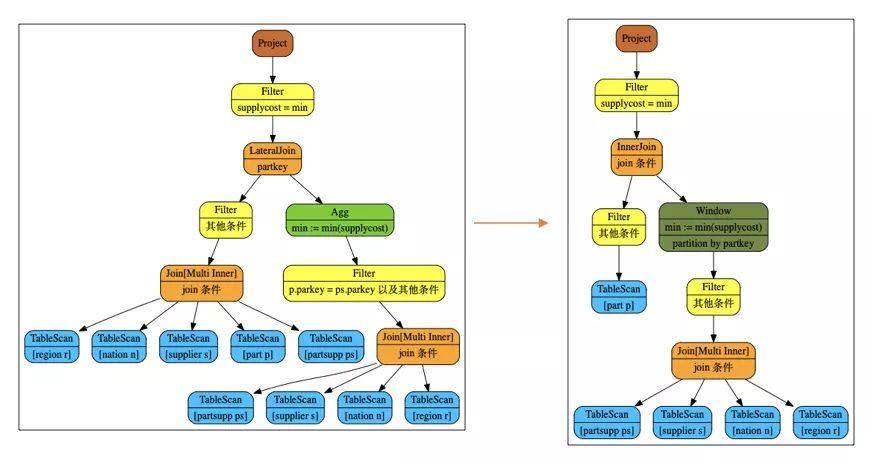
这里之所能改写成window是因为外部查询包含了内部查询全部的表和条件。而且agg函数min也满足特性agg(Ø)=agg(null) （如果不满足，需要对行进行mark以及用case when 改写输出）。

可以看到改写后tablescan的数量大大减少。更进一步，优化器后面的优化规则会进行根据primarykey的信息以及agg函数的特性进行join 和 window的顺序交换从而进一步减少window算子输入的数据量（filter-join pushdown）。

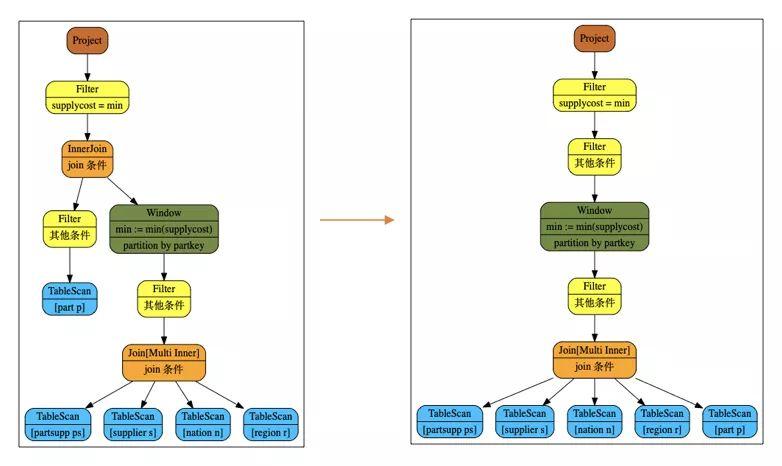
这些好处很多文章里都说了。我们在这里讨论一下这样改写的不好的地方：

• 比如在pk未能显示提供/agg的函数对duplicates敏感的情况下，window算子会阻挡filter-join的下推，从而打断了joingraph造成join的中间结果变大。
• 如果改写为两棵子树的join，filter-join可以下推到其中一颗子树上。而进行window改写后，filter-join无法下推。
• 在pipeline的执行模型下/&使用cte的情况下，扫表获得的收益有限。
• 传统优化器对join&agg的优化处理/优化规则比对window好/丰富很多。

综上所述，什么时候使用window进行改写关联子查询需要进行收益和代价的估计。

CorrelatedJoin在外部查询中的下推

在将correlatedJoin往子查询方向下推之前，我们会将correlatedjoin先在外部查询中进行下推(比如推过cross join等)。

这样做是因为correlatedJoin永远不会造成数据的膨胀，所以理论上应该早点做。但实际上correlatejoin下推后也可能切割joingraph，从而造成和window改写差不多的问题。

4 等价列的利用

如果在子查询中存在和外部等价的列，那么可以先用这个列改写子查询中的关联列减少关联的地方从而简化查询。下面举一个简单的例子。

Select t1.c2
From
  t1
Where
  t1.c3 < (
    Select min(t2.c3)
    From t2
    Where t1.c1 = t2.c1
    group by t1.c1
  )
  
-- 在子查询中使用t2.c1 代替 t1.ct进行简化

Select t1.c2
From
  t1
Where
  t1.c3 < (
    Select min(t2.c3)
    From t2
    Where t1.c1 = t2.c1
    group by t2.c1
  )

5 子查询相关的优化规则

一个方面correaltedjoin这个算子的特性给了我们一些进行优化的信息。下面举一些例子：

1. 经过correaltedjoin算子之后的行数与左子树的行数相同。
2. enforcesinglerow的输出为1行。
3. 外部查询的关联列决定(function dependency)correaltedjoin的新增的输出列。
4. assignuniqueid产生的key具备unique的属性等，可用于之后化简aggregation和group by等。
5. 子查询里的sort可以被裁剪。

另一个方面，在子查询的改写中，可以通过属性推导进行子查询的化简。比如：