微软搜索引擎 Bing 的核心技术 BitFunnel 原理讲解

导语

从90年代中期开始，人们普遍认识，对于内容索引来说，文件签名技术比反向链接效果更差。最近几年必应搜索引擎开发与部署了一套基于位分割的标签索引。这种索引（也称BitFunnel）替代了之前的基于反向索引的生产系统。这项转移背后驱动的因素是反向链接需要运转存储代价。本篇内容将讲述这项算法上的创新发明，改变传统上在云计算框架上被认为无法使用的技术。BitFunnel算法直接解决四项基础位分割块签名的限制。同时，算法的映射进入集群提供了避免和其他签名联系的代价。这里会先展示这些创新产生了比传统位分割签名的更显著的效率提升，然后将会进行BitFunnel与分块化Elias-Fano索引,MG4J,和Lucene等的对比。本文根据论文《BitFunnel: Revisiting Signatures for Search》和Bing团队实践分享视频，对BitFunnel原理进行分析解读。

问题背景

假设我们一篇非常短的文档：内容仅仅“big brown dog”这三个单词，我们可以用固定长度的位向量对这组单词进行编码，也称固定长度的位向量为文档签名或者布隆过滤器。简单样例这里采取了十六位长度的位向量来进行操作，当然，在Bing系统上不会用这么短的位向量，往往使用五千个以上的来进行表示。一开始，位向量全都是空的，因为还没有进行数据的加载操作。

布隆过滤器初始化会设置哈稀函数的种数，哈稀函数是为了让文档单词对应到位向量的固定位置上。这里我使用了三种不同的哈稀函数来映射。映射结果如下：

从上图可知，每个单词都对应着位向量上面的三个位置上置1，然后我们得到了这份简易文档的文档签名，假如我们要搜索“cat”单词在不在这份文档里面，我们只需要查询“cat”单词经过哈稀函数映射出来的三个位置上是否都为1就可以进行判定了，很明显，有一个不为1，所以“cat”单词并不在这份文档里面。

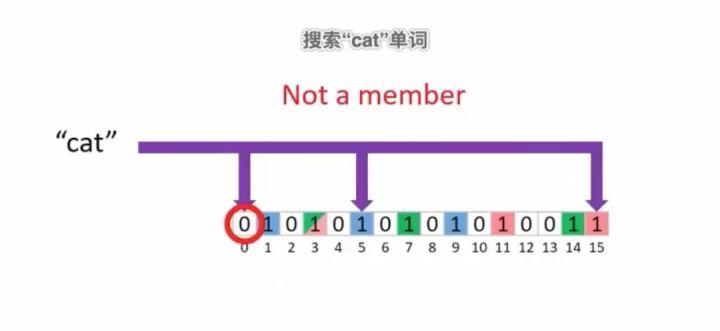
当我们搜索"big“单词时，我们会发现三个位置均置为1，那么我们可以判定“big”是这份文档的可能成员。如下图所示：

细心的你肯定注意到这里用了可能两个字，为什么是可能成员呢？下图是我们搜索的是“house”单词的结果：

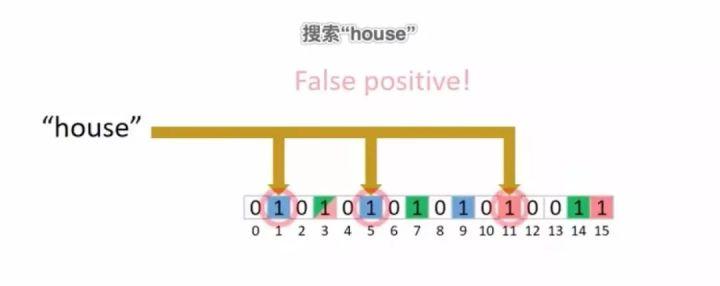
我们会发现这个单词的所有映射位置也都是1，但实际上我们知道文档里并没有“house”单词，这个存在的原因是因为有哈稀函数映射碰撞的存在，导致其他的位置也有相对应的1在文档里面补充了没有为1的情况，这也是我们为什么要用多种哈稀映射函数的原因，能够降低这种错误率。

基于这样的结构我们，假设我们存储有十六篇文档：A－P，依次建立了签名，那么有搜索需求：Query文档（包含多个单词）进来，通过下列查询就可以得到可能匹配文档：

这样的思路无疑是非常直观简单且容易实现的，但是在网络中存储的那些网页，基本需要几千位长度的位向量去表示，如果我们每一篇文档都这样去查询匹配，假设我们有N篇文章，用了P个位的文档签名标记，我们的计算机CPU每次处理的位数为64位，那么查询一篇文章需要花费的代价就是 N＊（P/64）单位时间。

这样的代价无疑是非常高昂的，因为现在文章的数量和长度乘积无疑是一个天文数字。一个非常巧妙的办法就是将这个矩阵反转过来，行列倒置，那么我们的存储由N＊P行列矩阵就变成了P＊N，很显然，P远远小于N。那么，我们的查询文档Query对应的只需要去匹配其中位为1的对应的文档的行向量即可，过程如下：

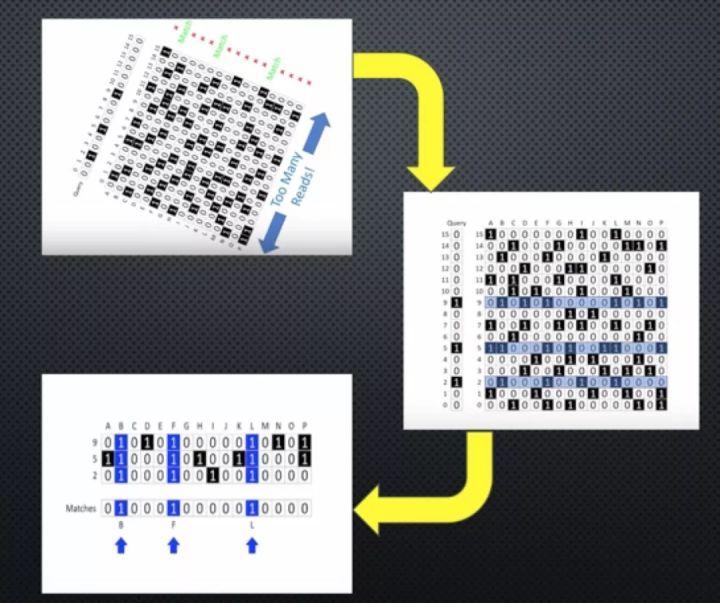
从上图流程可以看出，对应的只需要查询对应为1的位向量行数的文章的情况就可以了，假设真实中查询的文档Query的为1位数是W位，在现实查询中，W往往是少数几个单词去查询，W远远小于P，对应列进行并运算，结果为1则该篇位置可能匹配，这样查询速度就大大提升。但是，还有一个问题就是现实中 N 的数量也非常庞大。

那么这点如何处理呢？这就引进了今天要讲的重点算法：BitFunnel。

BitFunnel发明等级行

等级行是原始行的简单压缩版本，能够提高过滤速度，但同时也带来了更高的错误率，让我们看看等级行是怎么运行的。我们将原始行称为0-等级行，假设原始行是32位长度，那么1-等级行就是由0－等级行对等截成两半进行或运算获得，那么长度就降低了一半，更高等级行依此进行计算获得，如下图举例所示：

那么现在我们怎么使用我们获取的等级行呢？假设我们有3行32列需要匹配处理，那么我们可以考虑将第一行压缩成2－等级行，第二行压缩成1－等级行，第三行保持不变。如果我们没有这样做，我们需要将3*32＝96位全部放进内存进行查询处理才可以完成。而现在，（8+16+32）＝56位，详细如下图所示：

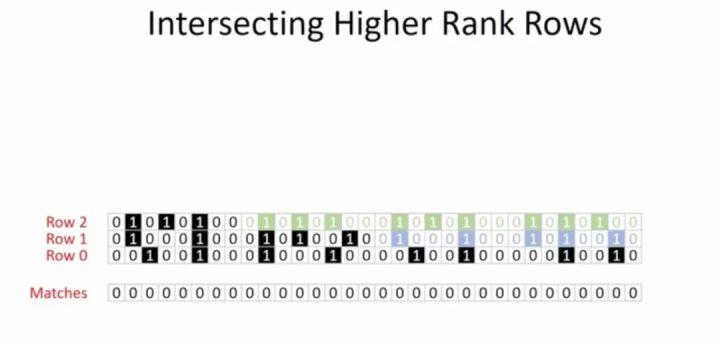
那么查询的时候，我们先将得出第一行和第二行的并运算结果，仅两列需要去与第三行在进行处理，然后平移到第三行另一边处理，再将第一行移动到第二行的另外一边，这时候也是两列均为1出现，然后与第三行处理，再转移回去处理最后一次即可得出结果，四次处理计算流程如下：

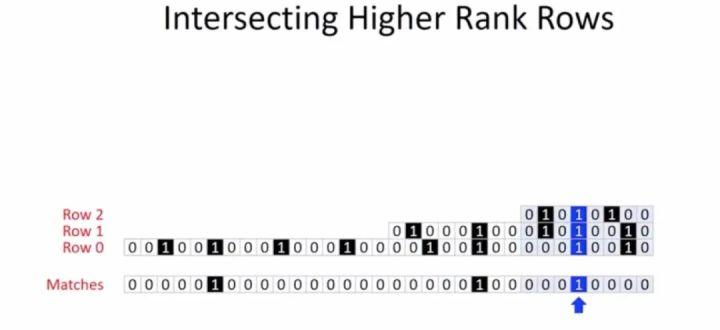
以上这样的处理我们可以大量地利用中间结果加快计算。

频率布隆过滤器
传统的布隆过滤器需要花费超长度的位向量才能做到满足较低的错误率，而BitFunnel则使用频率布隆过滤器来降低内存总量。什么是频率布隆过滤器？当我们在布隆过滤器中查询仅仅查询一个项目时，假设整个布隆过滤器为1的密度为10%，那么当我们只使用一个哈稀函数（假设哈稀函数是完全随机哈稀函数），那么对应的碰撞率为10％，那么随着我们哈稀函数种类的增加，我们可以计算出错误率,d为布隆过滤器的概率密度，但这里我们可以进一步提出新的概念信噪比：

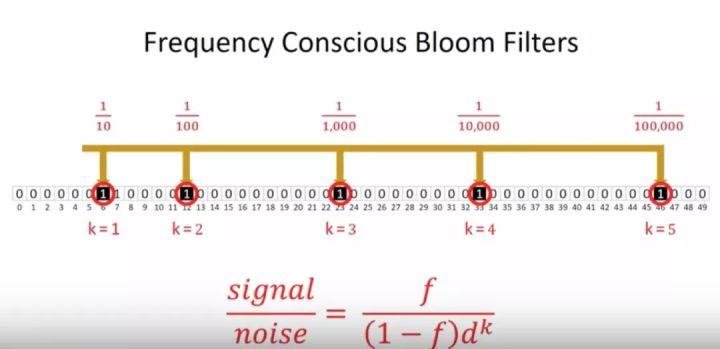
noise是我们经常用的错误概率（假阳率: Fasle Positive Rate, FPR），然而很少人去关注信噪比概念。让我们举例一些实际查询项目下的信噪比值：

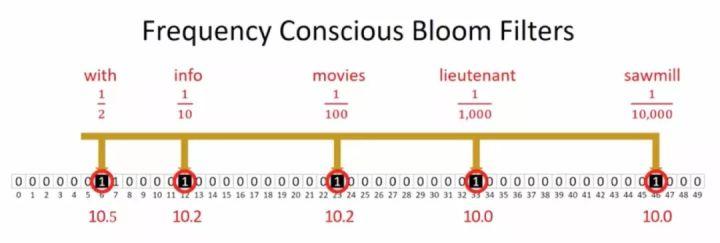
信噪比给我们的启示是：假设我们查询的是"with"单词，出现的频次约为50%，如果只有一种哈稀函数，那么它对应的信噪比分数为(0.5/((1-0.5)*${0.1}^1$)约为10.2，那么，当“info”单词，频率约为10%时，那么错误率与频率相等下，信噪比下降，随着频率的下降，布隆过滤器密度会突出，提高了这些稀少单词的错误率，因此就需要为这些稀少单词增加更多的哈稀函数从而才能保持与高频词一致的信噪比，举例只是到了“sawmill”单词，但现实互联网情况下，更小频率出现的单词非常多，往往需要10个以上的哈稀函数才能保持可接受的错误率。
就像查询DNA里面的特定稀少片段，传统的布隆过滤器做法是默认设置许多的哈稀函数和占用大量位数空间才能保障准确率。因此BitFunnel使用 Frequency Conscious Bloom Filter , 不同频次的单词使用不同种数的哈稀函数搜索匹配。
那么等级行在这种应用下怎么使用从而降低搜寻时间？BitFunnel结合了搜寻单词的频率和错误率的概念，提出了一种新的处理方案。

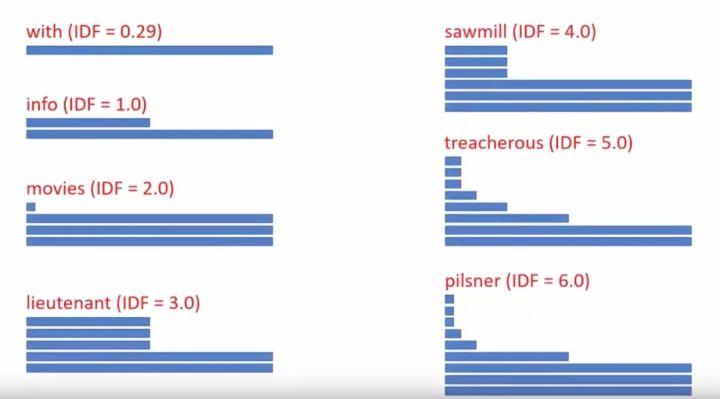
处理方案事实上就是用等级行数来关联我们单词：假设单词"with"的反向文档频率为0.29，那么用单条长度的原始行表示即可，“info”的为1，则用单条原始行还有一条1-等级行表示，后面则越稀缺的单词，其IDF越高，我们就用更多的行来表示其解决方案。你可能会问这些单词项目处理方案后面是不是存在简单的模式？然而我们也不知道具体答案，我们过去使用BF算法来通过确定的信噪比排序处理方案，同时也权衡查询时间和内存总量。最终出现了十亿中不同的解决方案，我们只评价了每种方案的IDF值，这一步花费了几秒钟，然后配置在系统中。

那么，让我们试试搜索一下“treacherous movies”是怎么进行查询的：

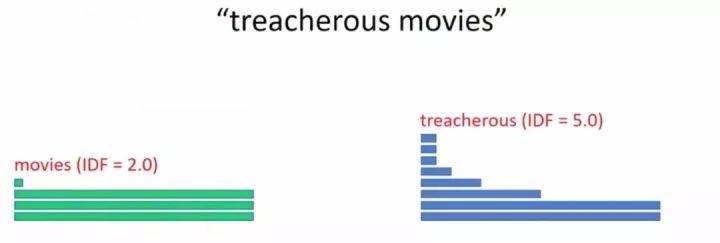
取出这两个单词的配置解决方案，然后将这两个解决方案组合起来获得下图（形状如漏斗）：

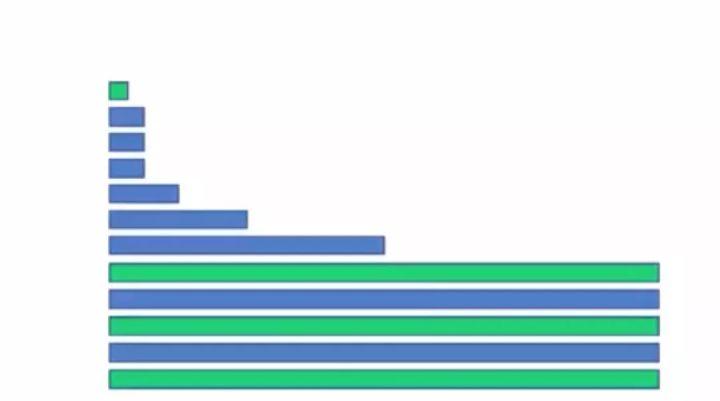
那么我们就可以简单直接地看出BitFunnel为什么能够这么快了：

假设行的概率密度为0.1，那么我们可以迅速前面四行就忽略了95%的列数。

集群间分享
以上的两种概念（等级行以及 Frequency Conscious Bloom Filter）让我们节约了大量的内存空间以及提高了查询效率。现实中我们的文本物料在现在互联网上已经是一个庞大的天文数字，以前还可以在单机上处理，现在已经无法单机处理，我们需要将庞大的矩阵切割出来放到不同的集群上处理，那么我们怎么做呢？
假设我们还是一共有十六篇文档和十六位的表示，那么矩阵表示为16*16，同时我们反转得到了十六位＊十六篇，我们可以知道，短文章的文档里面为1的个数还是相当少的，属于稀疏矩阵，会浪费相当大的空间存储，而长篇的文章里面1的个数相当高，其对应的错误率也很高。在BitFunnel中,集群间按不同文章的长度进行切割分享，下面例子切割成了三部分，实际上会按其他十到十五种不同组。

当按长度分好组后，我们就可以对稀疏部分进行压缩存储，密集的文章进行扩充位数存储，降低错误率。

那么随之我们跟之前一样就可以，当我们的查询文档Query对应只有三位为1是，我们分别对这三组的对应行求与运算即可得出结果：

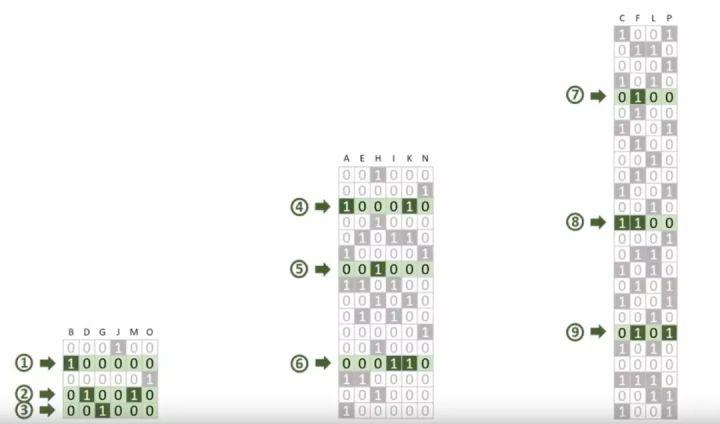
这样的计算方式实际上在90年代的时候就提出来了，但是一直不被认可。为什么？当时普遍都还是在单个计算机上进行各种算法操作，那么在一台机器上又将数据如上图一样切割成三部分分别进行处理很明显代价得不偿失。原本只需要进行一遍操作的流程被复杂化了，而且事实上也不仅仅分割成三部分，往往是十几类。而随着时代的发展，我们现在拥有了分布式的集群，我们可以将不同的机器处理不同文章长度种类的文档：

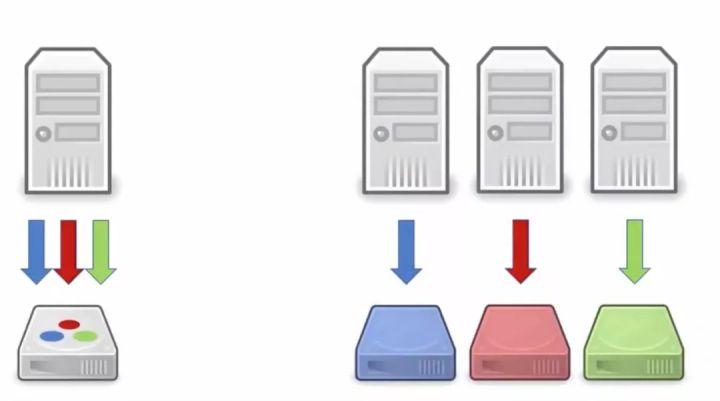
其次还有不同的是内存技术的发展，以前我们用每GB的花费金钱来衡量其中的成本是错误的方式：

传统衡量方式上，硬盘获得存储1GB的空间只需要0.05美元，而DDR4需要7.44美元，导致了大量企业认为能够增加存储就不断往硬盘上堆积，但这种方式很明显是错误的。

假设公司有存储数据总量为D，然后服务上需要查询的文档总量设置为Q，如果我们使用快速的机器，Q个查询很快就完成了（Q量可以通过广播的方式放进内存去各个数据分块中快速查询然后累计返回）：

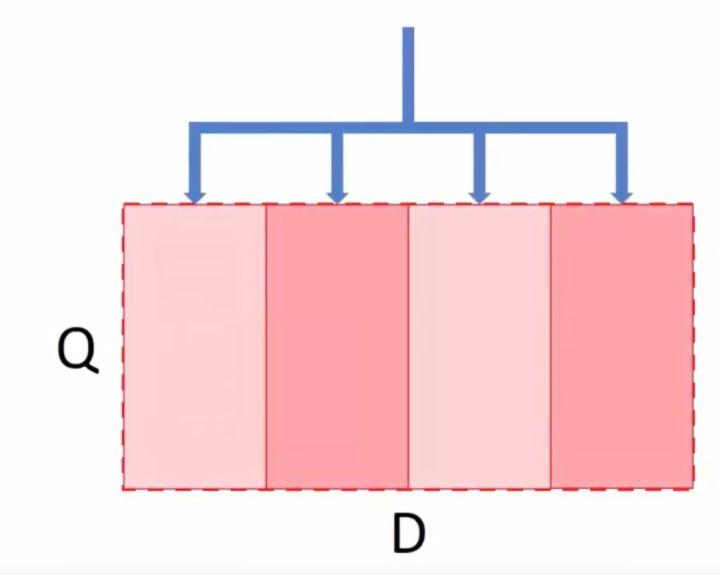
如果我们用存储大但是处理速度慢的机器，我们仍需要遍历所有的数据才能获得想要的数据总量：

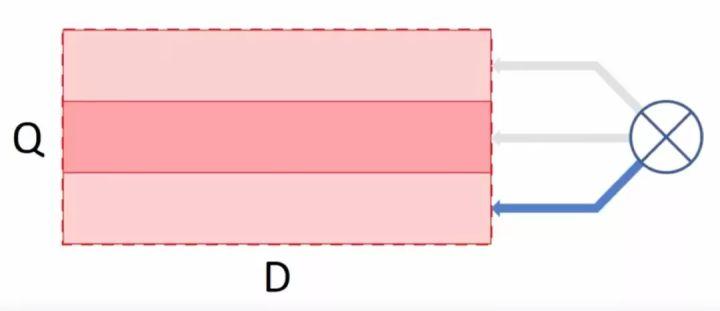
如果我们采用BitFunnel的方式来处理，那么，查询量Q可以用(带宽/总量)表示，引入这样的概念就可以讲之前硬盘和DDR4换一种计算方式，用每秒查询带宽量以及每美金每秒查询带宽量来表示之间能力差别，结果如下：