
从宏观模型原理到细节代码实践,深入浅出上手Transformer
序言
本文都会以用Transformer做中英翻译的具体实例进行阐述。
从宏观逻辑看Transformer
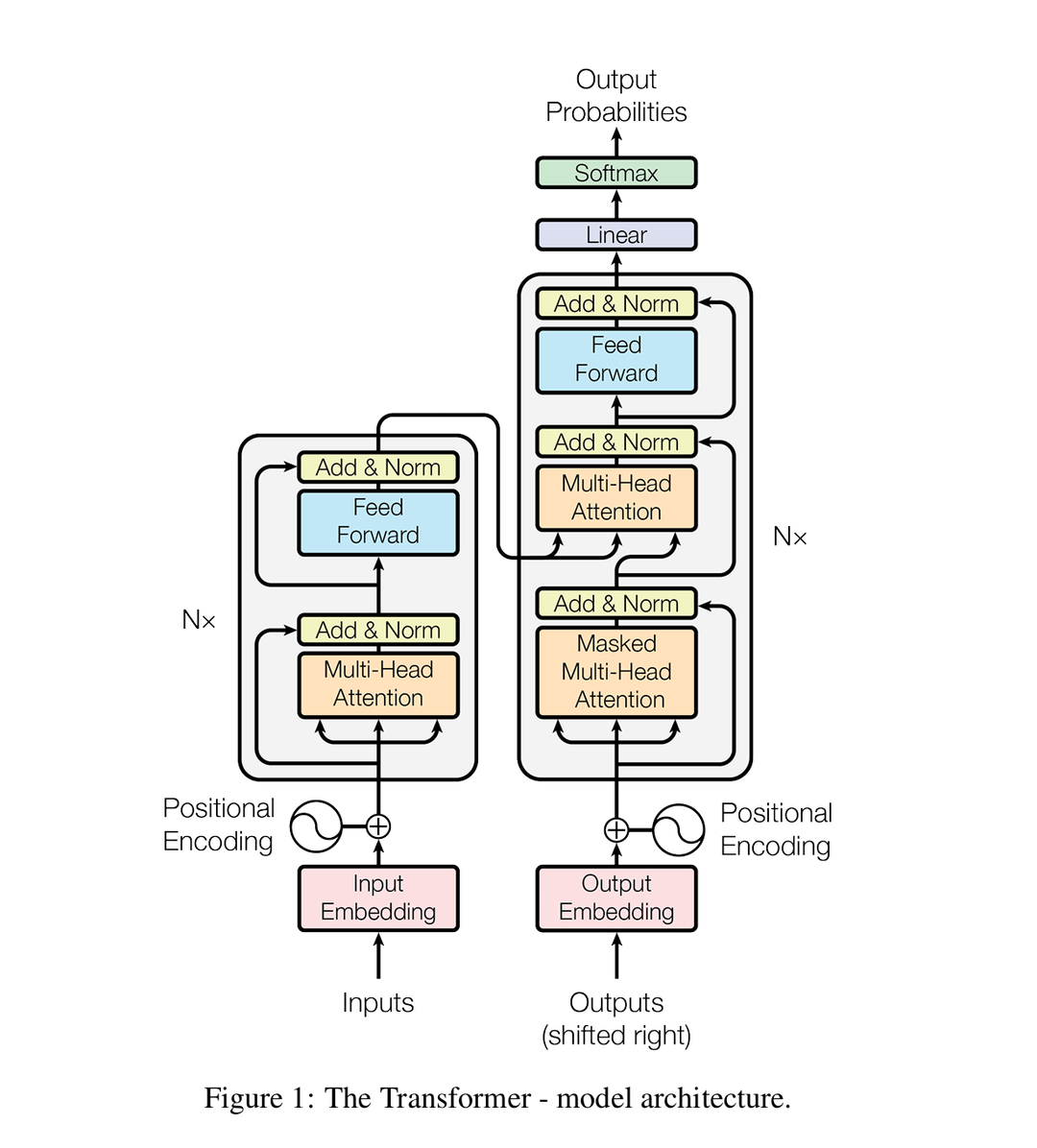
让我们先从宏观角度解释一下这个架构
首先 Transformer也是一个神经网络,神经网络的本质是模拟人脑神经元的思考过程,数学上是一种拟合,当然,人脑内部的信号处理是否连续或者可拟合我们不得而知,但Transformer在我的机器上实实在在地思考并输出了正确的答案。
Transformer 主要是设计用来做翻译的,分两大块,如上图,左边的编码器和右边的解码器。
编码器负责提取原文的特征, 解码器负责提取当前已有译文序列的特征,并结合原文特征(编码器解码器的连线部分),给出下一个词的预测。
GPT基本可以认为就是Transformer的解码器部分。
接下来我们分几个部分逐步讲解并附上代码实践,很长 得慢慢看....
输入和输出
我认为大部分文章都没有把输入和输出讲得很细,其实理解了输入输出,你就基本可以理解Transformer的大半了。
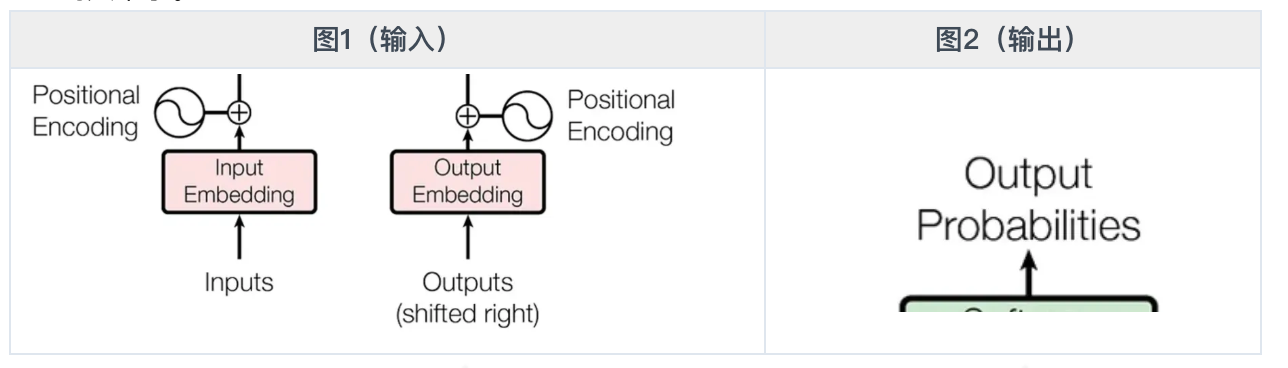
模型的输入
以中英翻译为例,Transformer的输入分两部分
- 源文序列(中文) 即图1左侧部分,输入到编码器。 举例: 我爱00700
- 目标译文(英文)即图1右侧部分,输入到解码器。 一开始只有一个,仅用于告诉模型开始翻译
模型的输出
很显然,对于上述输入,我们期待的输出是 I love 00700
的作用是表示翻译结束,因为翻译的英文不一定和输入的中文等长,所以需要有一个结束符。
模型并不能一下子输出完整的句子,他是一个词一个词( /token/ )吐出来的,并且每一个词都需要作为下一词的输入,这也是为什么大模型都是打字机交互的原因。 具体例子:
第一个循环
编码器输入 我 爱 00700
解码器输入 <bos>
输出 I
第二个循环
编码器输入 我 爱 00700
解码器输入 <bos> I
输出 love
第三个循环
编码器输入 我 爱 00700
解码器输入 <bos> I love
输出 00700
第四个循环
编码器输入 我 爱 00700
解码器输入 <bos> I love 00700
输出 <eos>
// 输出了结束符,翻译完成请注意上述是为了简化理解的一个陈述,实际上模型真正的输出并不是一个词,而是整个 /词表/ 内任意一个词可能的概率,也就是图2所示的probabilities。
具体说,就是一个数组[0.2, 0.7, 0.1], 序号为0的词的概率是0.2,序号为1的词的概率是0.7,序号为2的词的概率是0.1。 假设这是第二轮循环,词表是[I, love, 00700] 取最大概率0.7的词,然后得到第二轮输出是love, 和第一轮输出拼起来就是 I love。
词表 & token
划线的两个词 /token/ /词表/ 你可能仍有疑惑。这正是我们真正弄清楚整个输入输出的关键。
显然,计算机只能理解二进制数据,我们说输入"我爱00700"的时候,实际上输入的是处理好的二进制数据。
如何把句子转化成模型可以理解的二进制数据呢? 不妨先想想我们怎么学英语的, 没错,背单词啊! 我们需要先认识词,然后理解句子,模型也是一样的。
我们背的英文单词表,和这里的模型 /词表/ 其实是一个意思,当然,形式略有不同。 词表里的每一个词,就是我们说的 /token/ ,请注意 token 不一定是一个英语单词。 上述例子的英文词表可能是: [I, lo, ve, 00, 7] 。 显然,token不是按照空格分的。 原因是算力难以覆盖,英文单词有几十万个(不权威),老黄听了都摇头 。 而更低维度的分词,可以压缩词表的数量,[I, lo, ve, 00, 7]是我瞎写的,理解意思就行,让DS给我们举一个更好的例子:
假设语料库包含以下高频单词:
- play (10次)
- player (8次)
- playing (6次)
- plays (5次)
- replay (7次)
- replaying (4次)
直接按空格分词会生成独立词表:
空格分词词表大小:6
[play, player, playing, plays, replay, replaying]
# bpe分词算法最终词表(目标大小=4)
# Ġ表示这个token只会出现在开始,想一想 还原句子的时候你需要知道两个token是拼起来还是插入空格
[Ġplay, re, ing, er]对比空格分词, /bpe分词算法/ (想了解的自行ds,限于篇幅不赘述)可以有效压缩词表大小,在大量语料的情况下会更明显,40GB数据的GPT2也仅5w词表大小
嵌入
(embedding)
现在,我们有了词表,很容易就可以得到二进制的序列了
还是老例子:
我 爱 00700 被编码为 [1, 2, 3] (为了方便,这里假设分词就这样。)
我们可以直接输入到网络训练了吗? 答案是否定的,不过我们也终于来到了有意思的地方。 在在训练之前需要做一个 /嵌入/
来一个youtobe的动图看下 /嵌入/ 大概是啥。

再来一个DS的灵魂解释:
嵌入(Embedding)的核心思想是 将复杂、高维的数据(如文字、图像)转化为低维、连续的数值向量,同时保留其内在的语义或关系 。这种转化让计算机能像人类一样“理解”数据的含义,并用数学方式计算相似性、分类或生成。
额... 有点抽象,似乎讲了些什么,又似乎什么都没讲......
没关系,让我来举一个形象的例子 观察下面的句子:
红色
当红明星
生意好红火啊注意"红"这个字,发现了吗,在不同语境(或者说维度)它有不同的意思,如果我们直接输入token编码,这些信息是缺失的,模型就不太可能理解句子的意思。
那么,一个字或者说一个token到底有多少维度的语义呢?不知道啊 ,但是没关系,猜一个, 512。 没错,就是这么朴实无华!
于是我们就有了
- 嵌入矩阵
- : 嵌入维度(embedding_dim,如512)
即E是一个32000x512的二维矩阵 (代码里就是数组)
E[1,1] E[1,2] ...... E[1,512] 的值表示词表中序号为1的词在维度1、2、512的语义, 由此同样一个“红”的token,就可以有多种语义,这样模型就可以理解词和句子了。
当我们输入 我 爱 00700 被编码为 [1, 2, 3] , 实际上我们应该输入:
请注意请注意,所谓一个字有不同维度的语义,是我现编的比喻,如果它帮到你理解这个东西那最最好,如果觉得比喻得不太对,大可一笑了之。
继续
E[1,1] E[1,2] ...... E[1,512] 我们可以把它看作是以原点为起点的 512维的向量
,一般就叫做词的嵌入向量,也就是平时可能听到的向量化,没什么高大上的对吧。 向量化之后可以做什么呢?看图
(以三维举例,512维可以发挥想象力自行脑补)
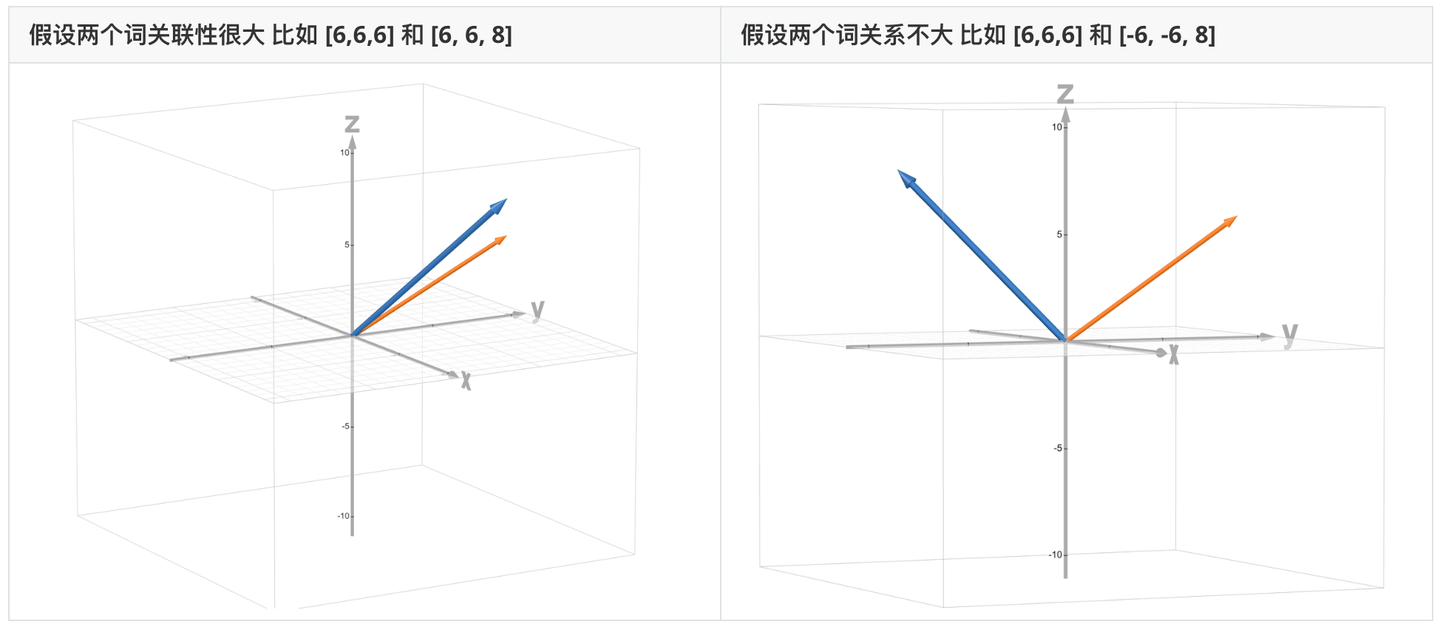
| 假设两个词关联性很大 比如 [6,6,6] 和 [6, 6, 8] | 假设两个词关系不大 比如 [6,6,6] 和 [-6, -6, 8] |
|---|---|
为了让模型理解词和词的关系,我们用数学语言去描述这种关系,就是向量的内积:
- 是两个向量之间的夹角
就算忘记了向量内积怎么算也没关系,我们只需要理解,夹角越小,向量内积越大, 两个词的关联越紧密就行了。 实际上大部分复杂公式的计算都是封装好了的。 这里的内积,在自注意力的时候我们也会用到。
到了这里就可以解释一下
的元素值是怎么来的了,我们定义了每一个词有512个维度,那么每一个维度的值是什么呢?
答案是模型自己学习出来的,E是模型的参数的一部分,一个词每个维度的值,初始化是一个随机值,模型训练的时候会被更新。
怎么学出来的? 试想一下: 语料里面有无数的词,但是他们是有一定的关联的,比如 I love 这两个词经常同时出现,那么他们的内积就应该较大,反之也一样。实际上有点像聚类,怎么理解都行,模型学得差不多的时候,token的分布或者说嵌入向量的关系,一定是有规律的。
让我们来用数学语言总结一下嵌入:
就是我们的查表或者说嵌入操作:
- 输入张量 x \in \mathbb{R}^{B \times L}
- B: 批次大小(batch_size)
- L: 序列长度(sequence_length)
- D: 嵌入维度
嵌入查找操作 y = E[x] \in \mathbb{R}^{B \times L \times D} 上述例子 就是 x = [1, 2, 3] ,L是句子长度也就是3
为什么这里也会叫查表? 实际上对索引为1的token做嵌入,就是在嵌入矩阵里到找第一行然后拿出来,就是 E[1,1] E[1,2] ...... E[1,512] 。这个过程不就是查表么。
Batch 处理
细心的你可能发现了问题,这里多了一个维度B,输入的结果 y=B \times L \times D,是三维的。这里解释一下,我们的例子只有一句话,但是在模型的训练中,其实是一次性输入多句话并行计算的,batch_size 的值就是你一次性输入多少句子来训练,一般来说,这取决于你的显存大小,自行尝试调整就可以了。
假设batch 为2,一次输入两句:
[1, 2, 3] (嵌入)=> \left[ \begin{matrix} E[1,1] & E[1,2] ...... & E[1,512]\\ E[2,1] & E[2,2] ...... & E[2,512] \\ E[3,1] & E[3,2] ...... & E[3,512] \end{matrix} \right] \tag{3} "> [1, 2, 4] (嵌入)=> \left[ \begin{matrix} E[1,1] & E[1,2] ...... & E[1,512]\\ E[2,1] & E[2,2] ...... & E[2,512] \\ E[4,1] & E[4,2] ...... & E[4,512] \end{matrix} \right] \\">
两句话的embedding矩阵合并,得到一个 2x3x512的三维矩阵 就是我们给编码器的输入了。 此时 B=2 L=3 D=512
\left[ \left[ \begin{matrix} E[1,1] & E[1,2] ...... & E[1,512]\\ E[2,1] & E[2,2] ...... & E[2,512] \\ E[3,1] & E[3,2] ...... & E[3,512] \end{matrix} \right] \left[ \begin{matrix} E[1,1] & E[1,2] ...... & E[1,512]\\ E[2,1] & E[2,2] ...... & E[2,512] \\ E[4,1] & E[4,2] ...... & E[4,512] \end{matrix} \right] \right] \\
padding掩码矩阵
还没完,让我们来一点刁钻的问题。 上述例子L=3,两个句子长度都一样=3。 如果句子长度不一样呢?batch矩阵岂不是拼不出来? 当然不会,实际写代码的时候,L一般都是取一个较大值,比如语料中最长句子的值。L=100。 不够长的句子怎么办呢? 补padding,注意不是0,因为神经网络的某些中间计算如softmax输入0也是有值的。 一般是用一个特殊的token作为padding。
在自注意力计算的时候(下文会讲)会根据padding的位置,生成mask 矩阵,计算时候padding替换为一个极小值比如-1e9,就可以不影响计算了。
PositionalEncoding
现在这个带padding的矩阵可以输入模型开始训练了吗? 还是不行..... 我们还缺少一个重要的信息,位置。 举一个例子:
[ [0.3, 0.5, 0.1, 0.4]
[猫,吃,鱼] => Transformer => [0.1, -0.6, -0.2, 0.3],
[0.3, 0.5, 0.3, -0.1] ]
[ [0.3, 0.5, 0.1, 0.4]
[鱼,吃,猫] => Transformer => [0.1, -0.6, -0.2, 0.3],
[0.3, 0.5, 0.3, -0.1] ]很明显,虽然只是交换了一个字的顺序,但其实是两个完全不同意义的句子, 而 Transformer输出的分布却是不变的,说明网络没有办法识别位置信息。
为了解决这个问题,Transformer的论文里的方案是添加位置编码,也就是PositionalEncoding。
其实没有那么神秘,我们把 Transformer 看成函数
, 现在的问题是:
我们可以加上一个位置编码
去规避这个问题
- : 当前的位置序号
来一个简单粗暴易理解的 P(i) = i
猫 0
吃 1
鱼 2然后呢?就是简单的直接加上去
\left[ \begin{matrix} E[1,1] + 0 & E[1,2] + 0 ...... & E[1,512] + 0 \\ E[2,1] + 1 & E[2,2] + 1 ...... & E[2,512] + 1 \\ E[3,1] + 2 & E[3,2] + 2 ...... & E[3,512] + 2 \end{matrix} \right] \\">
没错,这样其实我们的输入就包含了位置信息了,只要信息在那里,模型总能学明白
当然,这里只是为了方便说明位置编码本身,所以用了最简单的方案,你说它能不能跑,那肯定也是能跑的,就是会有不少问题,实际上论文里实现是正弦torch.sin(position * div_term)和余弦函数torch.cos(position * div_term)来生成位置编码, 解释起来就篇幅太长,大家可以自己探索。
位置编码不改变矩阵的维度,只是改变了数值, 我们给编码器的最终输入总结如下:
分词 => 嵌入 => PositionalEncoding => \left[ \left[ \begin{matrix} x_{1,1} & x_{1,2} ...... & x_{1,512} \\ x_{2,1} & x_{2,2} ...... & x_{2,512} \\ x_{3,1} & x_{3,2} ...... & x_{3,512} \end{matrix} \right] \left[ \begin{matrix} x_{1,1} & x_{1,2} ...... & x_{1,512} \\ x_{2,1} & x_{2,2} ...... & x_{2,512} \\ x_{3,1} & x_{3,2} ...... & x_{3,512} \end{matrix} \right] \right] \\">
但是对于解码器的输入,还需要额外处理,继续往下。
并行计算 & Teacher Forcing
回顾下一开始的例子
第一个循环
编码器输入 我 爱 00700
解码器输入 <bos>
输出 I
第二个循环
编码器输入 我 爱 00700
解码器输入 <bos> I
输出 love
第三个循环
编码器输入 我 爱 00700
解码器输入 <bos> I love
输出 00700
第四个循环
编码器输入 我 爱 00700
解码器输入 <bos> I love 00700
输出 <eos>
// 输出了结束符,翻译完成我们给编码器的输入始终是整个句子序列的embedding。而给解码器的输入,则是当前已经预测出来的 n-1个词的序列的embedding。
并行计算
当你真的上手去写代码的时候,你就会发现, 在训练阶段,代码里我们给解码器直接输入完整的句子 I love 00700 ,且模型输出直接就是整个句子。 只有一个循环。你现在肯定满脑子问号,直接输入正确答案了,还学什么?
别急,实际上我们输入不是全部的ground truth,是 n-1序列的ground truth。怎么理解呢?真正的ground truth 是 I love 00700 eos 。 我们的输入是 I love 00700。 当然这样仅仅是少了最后一个token的答案而已。
实际上解码的输入(姑且叫trg_input)在做计算的时候还需要做一个causal mask,叫做因果掩码,字面意思就是为了防止计算的时候知道未来的信息。
>>> trg_input # 假设我们的input长这样 1234代表 <bos> I love 00700
tensor([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
# 因果掩码矩阵是这样的,对角线上移一位的上三角矩阵,上三角的元素是极小值
>>> mask = torch.triu(torch.ones(4, 4), diagonal=1)
>>> mask = mask.float().masked_fill(mask == 1, float(-1e9))
>>> mask
tensor([[0., -inf, -inf, -inf],
[0., 0., -inf, -inf],
[0., 0., 0., -inf],
[0., 0., 0., 0.]])
>>>
#执行 causal mask
>>> trg_input + mask
tensor([[1., -inf, -inf, -inf],
[1., 2., -inf, -inf],
[1., 2., 3., -inf],
[1., 2., 3., 4.]])看看causal mask结果的第一行,[1., -inf, -inf, -inf] 其实就是相当于第一轮循环的输入 bos, 因为无限小在计算的时候可以忽略。 后续的2、3、4行刚好也就是 对应的2、3、4轮循环。 get到了吗, 直接作为一个矩阵输入,在模型里并行计算,4个循环优化成了一个!能够并行计算,这正是transformer一个重要特性。
Teacher Forcing
想一想为什么我们可以实现并行计算? 因为训练的时候,我们提前知道了正确答案,在生产环境推理过程中,我们不可能知道第一个token应该输出I,第二个token应该输出love ...., 所以推理的时候,只能顺序执行循环。
再多想一点,在训练的时候,模型还并不成熟,第一个字符输出的未必是I,假设输出了 He 呢? 然后第二轮循环我们的输入就是 bos He, 这样继续循环下去只会越来越错,非常不利于学习的收敛。 所以,我们第二轮循环不输入He, 而是用正确答案 I 来继续下一个token预测,实验表明这样学习的速度会更快。 这种训练方法,我们就称之为Teacher Forcing。
关于并行计算和Teacher Forcing感觉大部分文章都是一笔带过,而我感觉这里很重要,包括理解架构本身或者是去理解为什么transformer带来了技术的爆发,并行计算是一个很重要的因素。
输入输出的代码实现
作为一个严谨的工程师,最后我贴一下我自己的实现,并做简单讲解:
# 关于语料 我的数据集来自 wmt17 v13 zh-en 大约100m 30+w行长句子
# 从csv读出来, 第一列是中文 第0列是英文
train_data = read_tsv_file(opt.train_tsv, 1, 0, opt.delimiter)
valid_data = read_tsv_file(opt.valid_tsv, 1, 0, opt.delimiter) if opt.valid_tsv else []
test_data = read_tsv_file(opt.test_tsv, 1, 0, opt.delimiter) if opt.test_tsv else []
# 分词器初始化 我这里是bpe bytelevel 32000 词表大小,具体实现太长就不贴了
src_tokenizer_path = os.path.join(opt.data_dir, "tokenizer_zh.json")
src_tokenizer = train_tokenizer([src for src, _ in train_data], opt.vocab_size, src_tokenizer_path)
trg_tokenizer_path = os.path.join(opt.data_dir, "tokenizer_en.json")
trg_tokenizer = train_tokenizer([trg for _, trg in train_data], opt.vocab_size, trg_tokenizer_path)
# 有了分词器之后,对训练数据句子分词 打包成pkl格式,方便模型训练的时候读取
processed_train = process_data(train_data, src_tokenizer, trg_tokenizer, opt.max_len)
# train阶段
# 从pkl加载数据 略
# 训练输入
for i, batch in enumerate(dataloader):
# 准备数据 每次循环处理一个batch的数据
src = batch['src'].to(device) # 取出语料原文。我 爱 00700 (举例,实际上batch是多句的数组,但是矩阵运算的时候都是一起并行算的)
trg = batch['trg'].to(device) # 取出语料目标译文。bos I love 00700 eos
trg_input = trg[:, :-1] # 去掉最后一个token, bos I love 00700 n-1的Teacher Forcing序列
trg_output = trg[:, 1:] # 去掉第一个token, I love 00700 eos 真实的groud truth,用于计算损失
# 前向传播 清空梯度
optimizer.zero_grad()
# 输入模型计算一次
# teacher forcing: trg_input 实际上就是ground truth(正确的值)
# train 模式下,output是整个句子的预测值
output = model(src, trg_input)
......
# 嵌入
"""初始化嵌入矩阵"""
# 使用正态分布(高斯分布)初始化张量
# 均值为0,标准差为0.02
# 在数学上,512维的随机向量,可以认为是互相正交的(就是任意两个token之间一点关系都没有)
nn.init.normal_(self.weight, mean=0, std=0.02)
# 基本的嵌入查找
# weight 是模型参数,自动参与学习
embeddings = self.weight[x]
# mask
"""创建源序列和目标序列的掩码"""
src_padding_mask = (src == self.pad_idx) # src padding掩码
trg_padding_mask = (trg == self.pad_idx) # trg padding掩码
# 因果掩码
seq_len = trg.size(1)
trg_mask = torch.triu(
torch.ones((seq_len, seq_len), device=src.device), diagonal=1
).bool()
return src_padding_mask, trg_padding_mask, trg_mask
# 应用mask 我这里的mask是bool矩阵,true表示需要mask
# 如果mask是true,scores对应位置的元素就填充为极小值 -1e9
if mask is not None:
scores = scores.masked_fill(mask == True, -1e9)输入输出终于写完 看到这里就真的不容易 感谢~!
自注意力机制
到这里我们已经完成了输入的所有前置处理,训练数据开始进入到网络训练。 而理解Transformer网络的关键就在于自注意力机制,如下图所示的三个模块,他们是整个网络的核心。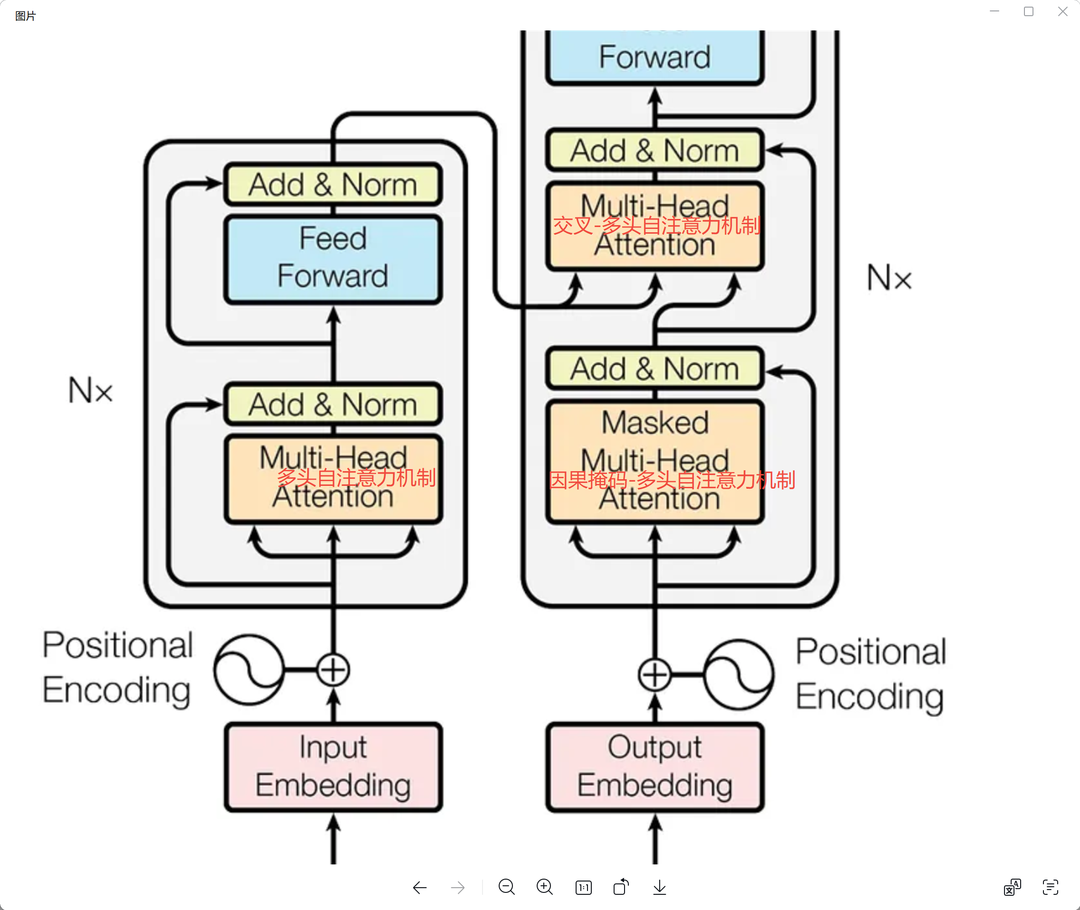
注意力机制
注意力其实非常好理解, 如下图: 万绿丛中一点红,你首先看到了红,这就是注意力。

在训练网络中,注意力的作用是什么呢?
老例子:“ 我 爱 00700 ” 翻译为 “ I love () ” () 为当前正在预测的词。
如上图, 前面我们介绍过Transformer预测下一个词的时候,会结合整个上下文,即“我 爱 00700 I love”,假如没有注意力机制,那么所有词对预测结果的贡献是一样的! 假设语料的言情文偏多,那输出很可能是 I love you, 很明显不合理, 此时我们希望网络把注意力集中在“00700”这个词上,其他词应该忽略掉。
那么在数学上注意力是什么呢? 非常简单,就是权重系数
写出来就是:
- x ∈ R^(seq_len, d_model) seq_len是句子长度,d_model=512是embdedding的纬度,忘了的话往回翻复习下吧
- W ∈ R^(512, 512) 是权重矩阵
??? 解释了这么久 就这? 没错是的 ♀️ 取个高大上的名字而已
自注意力机制
自注意力毕竟多了一个字,肯定还是有点不一样的,不一样在哪呢,他乘的不是权重矩阵,它乘它自己!
- 即权重
- x ∈ R^(seq_len, d_model) seq_len是句子长度,d_model=512是embdedding的纬度,忘了的话往回翻复习下吧
重点看一下这个
如果你对矩阵乘法熟,你马上就会意识到,这不就是句子的词和词之间的内积吗?
回忆一下嵌入的内容,我们说过词向量的内积反应的是词的关系远近。
本质是,Transformer通过句子本身的词和词之间的关系计算注意力权重! 所以我们叫它 - 自注意力 !还算自洽吧~
当然,直接相乘没有参数可以训练啊,来个线性变换吧 ,于是
不好记,得起个名字, 第一个式子是原始请求 就叫Query吧,简写为Q
感觉不用纠结这个命名,反正论文没提命名的道理 自行想象吧
第二个式子是被用来计算关系的,就叫Key吧,简写为K
于是:
按照论文所提,实验发现,QK点积可能会过大,数据方差太大,导致梯度不太稳定,所以需要把分布均匀一下,于是:
我们需要的是权重,所以需要转化为 0.0~1.0 这样的值,这正是 /softmax/ 函数的能力 于是:
代入
, y改写为Attention,更高大上
另外为了增加网路的复杂度,我们不直接乘x,老办法,线性变换一下, 记为V
最终
最终我们得到了和论文一模一样的公式~
多头注意力机制
先看一个图,这是一个自注意力计算的示例:
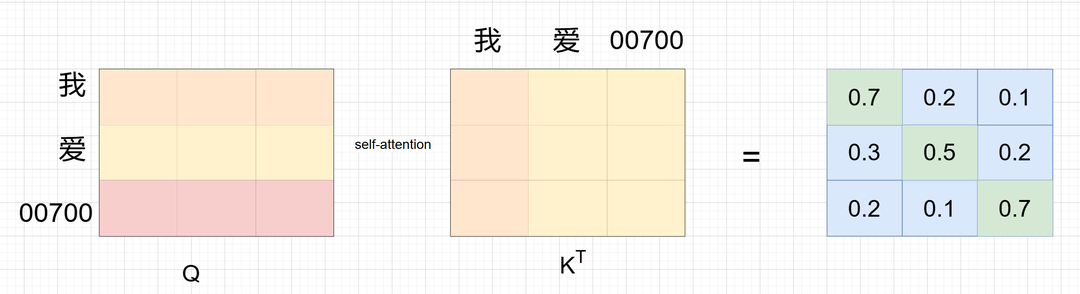
问题是: 我 - 我 爱-爱 00700-00700 的分数最高, 自己最关注自己,听起来是合理的,但论文作者应该是觉得这不利于收敛。 所以提出了多头机制
其实这里论文并没有太多解释,我理解是一种实验性的经验
那么什么是多头? 其实也很简单,就是分块计算注意力,好比原来是一个头看整个矩阵, 现在是变身哪吒三头六臂,一个头看一小块,然后信息合并。 画图说明:
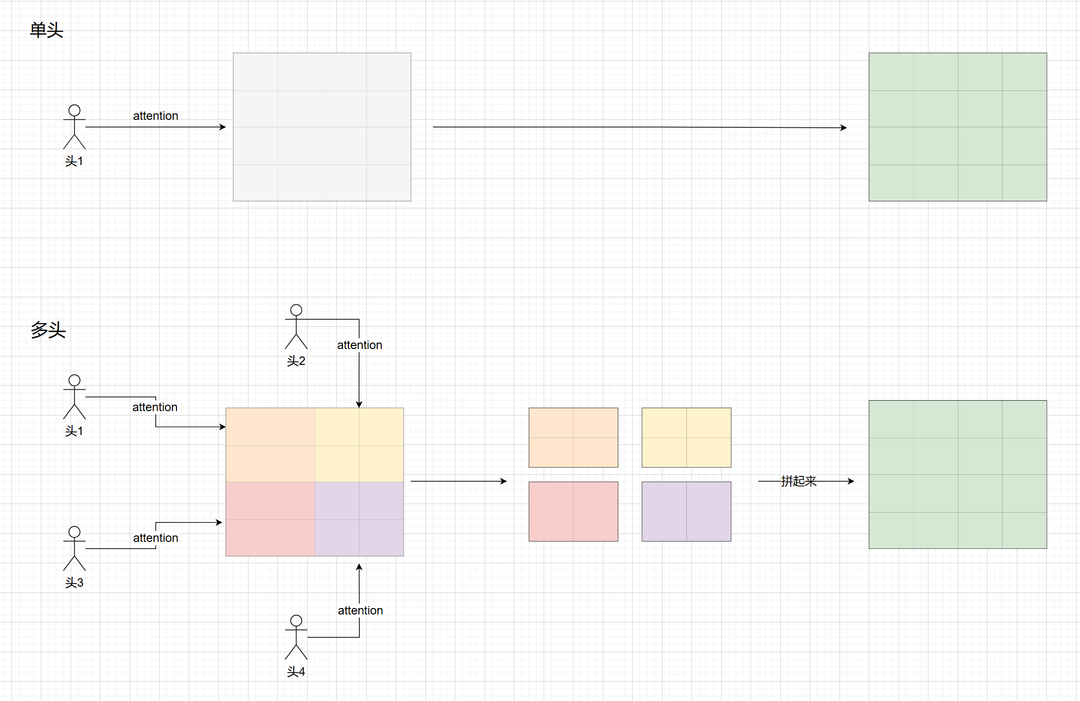
这种分头其实本质上计算量是一样的,只是注意力分块了,直接看公式就好了。
_
- Q, K, V 是输入矩阵,形状为 (batch_size, seq_len, d_model)
- W_i^Q ∈ R^(d_model × d_k)
- W_i^K ∈ R^(d_model × d_k)
- W_i^V ∈ R^(d_model × d_v)
- head_i 的形状为 (batch_size, seq_len, d_v)
论文中 i=8, 8个头, dk =dv = d_model/8 = 64
因果掩码-多头自注意力机制
其实输入输出的时候就讲了,就是解码器做多头计算的时候 使用teacher forcing,需要加上因果掩码mask。 下面代码说明。
交叉-多头自注意力机制
解码器如何结合编码器的上下文就在这里了,如果是交叉-多头自注意力机制,那么 Q = x, K=V=编码器的输出,直接看代码最直观。
本文系作者在时代Java发表,未经许可,不得转载。
如有侵权,请联系nowjava@qq.com删除。
