揭开DeepSeek-R1的神秘面纱：GRPO 核心技术详解

GRPO技术背景

GRPO技术其实不是在DeepSeek-R1中提出，早在DeepSeek去年2月发的一篇论文《DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models》中，他们就已经提出了GRPO技术，并用在DeepSeekMath模型上。为了更好的讲解这个算法的原理，我们首先得了解一些基本的强化学习概念，有相关基础的朋友可以跳过下一小节。

强化学习基本概念

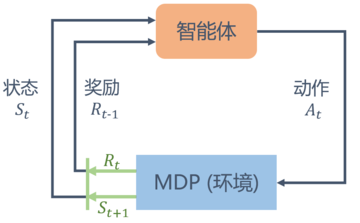
在强化学习中，我们通常会讨论下面的一个问题背景：一个智能体（agent）在某个环境中可以执行一些动作（action），它在执行某个动作之后会从一个状态（state）切换到另外一个状态，同时所在的环境也会给它一个反馈（reward），而我们的目标则是最大化这个agent在环境中所能获得的reward，如下图所示：

img

上面的问题背景通常被称为马尔可夫决策过程

（Markov decision process)，简称MDP。

既然说是马尔可夫决策过程，相信不少敏感的朋友会回想起马尔可夫随机过程。马尔可夫随机过程的一个重要性质就是：下一个时刻的状态只取决于当前状态，而不会受到过去状态的影响，即状态转移概率

。而在MDP中，下一个时刻的状态取决于当前的动作和当前状态，即

，因此被称为马尔可夫决策过程。

下面简单介绍一些非常重要的概念：

• S为状态空间，即所有可能状态的集合
  
• A为动作空间，即agent所有可能动作的集合
  
• 
  

为智能体采取的策略（policy)，策略是一个函数，表示在输入状态情况下采取动作是状态转移函数，表示在状态执行动作后到达状态为奖励函数，此奖励同时取决于状态和动作，并且为回报(Return)，它表示从时刻状态开始，直到终止状态时，所有奖励的衰减之和：
，其中为价值函数，它通常用来衡量agent处于某个状态s下的预期收益（不仅包含即时奖励，还考虑未来的奖励），通常我们用表示在MDP中基于策略为动作价值函数(action-value function)，用表示在MDP遵循策略时，对当前状态执行动作得到的期望回报：

同时状态价值函数和动作价值函数之间还存在以下关系：在使用策略

中，状态的价值等于在该状态下基于策略

采取所有动作的概率与相应的价值相乘再求和的结果

强化学习算法的种类

在强化学习问题中，根据是否知道环境相关的信息，我们通常把问题分为两类：model-based和model-free。model-based是指我们能提前知道奖励函数

和状态转移概率，反之model-free则二者都不知道。model-based的问题解决有一个固定的套路可以使用，就是dynamic programming（动态规划

），这里就不细说了。

在现实世界中，model-free形式的强化学习问题要更为常见。为了解决这类问题，我们通常有两类方法：一种是基于价值(value-based)的方法（例如Q-learning

和DQN），另一种是基于策略(policy-based)的方法。二者的主要区别是：基于值函数的方法主要是学习值函数，然后根据值函数导出一个策略，学习过程中不存在一个显式的策略；而基于策略的方法则是直接显式地学习一个目标策略。今天我们所要讲解的GRPO算法则是一种基于策略的方法。

从策略梯度算法

说起

GRPO算法本质上来说是从策略梯度算法发源而来，因此先给大家介绍相关概念以便于理解后面复杂的公式。

通常，在强化学习任务中，agent会不断地与环境进行交互直至最终结束，根据上述过程，我们可以得到一条轨迹，表示为

，其中表示状态, 表示行动，,

表示agent在状态1的时候选择了动作1，后面的以此类推，如下所示：

假设agent的策略网络参数为

，那么我们可以用

表示一条轨迹产生的概率：

在agent与环境交互的过程中，还存在一个奖励函数，当输入状态

和动作时，奖励函数会返回，我们把轨迹当中的所有奖励都加起来就得到了。策略梯度算法则是为了找到一个最优策略网络参数，使得越大越好，也就是最大化

的期望：

为了最大化这个期望值，我们会采用梯度上升的方式进行参数更新：

而事实上，最后推导出来的梯度项没有办法直接计算，通常使用采样

次轨迹

的方式去计算得到梯度：

但是这样会带来一个明显的问题，数据利用效率不高。每次参数更新前，都需要采样大量的数据，训练的时间开销全都集中在了数据采样上。为了解决采样时间开销大的问题，我们可以使用重要性采样

技术。

重要性采样通常被用来估计一个分布的期望值。从数学上来说，它的原理是通过不同分布的样本进行估计，然后乘上一个重要性权重（即两个分布概率的比值），这样可以无需从原分布中采样，用另一个简单分布的样本也能计算原分布的期望：

使用重要性采样的好处是，可以让我们使用旧策略

采样的数据，多次更新策略网络参数

，从而大大节省了训练中采样数据的时间开销：

事情到这里看起来比较完美了，但事实上，在使用过程中我们还会遇到一些问题：比如在很多游戏场景中，得到的奖励总是正的。如果所有动作的奖励均为正，那么策略更新时会盲目提高所有动作的概率（只是提升幅度不同），但无法区分哪些动作比其他动作更好，即缺乏相对比较。同时，还有可能引起高方差问题：原始奖励的绝对值差异极大，导致梯度更新的方差过大，训练不稳定。因此，我们通常希望奖励值有正有负，通过将奖励减去一个基线b，我们就能达到目标。而这个新的奖励值我们称为优势函数，基线b我们通常取所有动作的平均预期奖励

：

其中，

表示在状态下执行动作的预期累积奖励，表示在状态

下所有动作的平均预期奖励。最终，我们的优化目标便可以写成下面这样：

TRPO算法

和PPO算法

在理想情况下，如果我们能够采样足够多的次数，那么使用importance sampling估计得到的梯度和原梯度是相等的。但实际上，我们并不能采样那么多次数据，因此TRPO算法引入了置信域（trust region）的概念，避免和

差异过大而导致估计不准确。具体来说，TRPO算法给上面的优化目标加上了一个KL约束项：

由于上面的优化目标是一个带约束的优化问题，因此TRPO算法的求解会比较复杂，涉及到KKT条件，共轭梯度等方法，此处就不做介绍，感兴趣的朋友可以再去研究下。

TRPO算法求解的难度主要来源于它的KL约束条件。熟悉凸优化的朋友可能知道，求解带约束问题和无约束问题难度相差可是非常大。那么有没有一种方法，让我们既可以约束

和

的差异程度，又不将它作为约束条件呢。PPO算法采用将KL散度项直接加入到优化目标中，将有约束优化问题转化为无约束优化问题进行求解：

但是在实践中，上述算法又会引来另外一个问题，很难选择一个固定的常数

，使算法的效果比较好。因此，PPO算法又进行了进一步优化，引入了一个自适应的KL惩罚，给出一个KL的可接受区间，当KL项大于时，说明和 差异过大，就增大;当KL项小于时，就适当减小

。这个算法被称为PPO1算法。

是否还有更简单的方式去优化一个类似的目标呢？PPO的作者们又提出了一个更简化的版本：

这里的

的函数表示将限定在

的区间内。此算法被称为PPO2算法。在实践中发现，通常PPO2算法的效果会优于PPO1算法。

语言模型中的PPO算法

上面都是在纯强化背景下的PPO算法，那么在LLM领域，PPO算法又是如何应用的呢？通常来说，我们会构建四个模型：

• Actor Model

：它的作用是预估总收益，目的是学习一个值函数: 它的目标是计算即时收益，即学习奖励函数

• ；
• Reference Model: 它的作用是给语言模型增加一些约束，防止需要训练的语言模型训歪。

通常来说，在RLHF-PPO阶段，Actor/Critic model都是需要训练的，而Reward/Reference Model则参数冻结。我们通常采用下面的方式去初始化这些模型：actor/reference model采用sft阶段训练后的语言模型初始化，critic model和reward model则采用语言模型的backbone + 各自的value head来进行初始化。一个完整的RLHF-PPO训练过程如下：

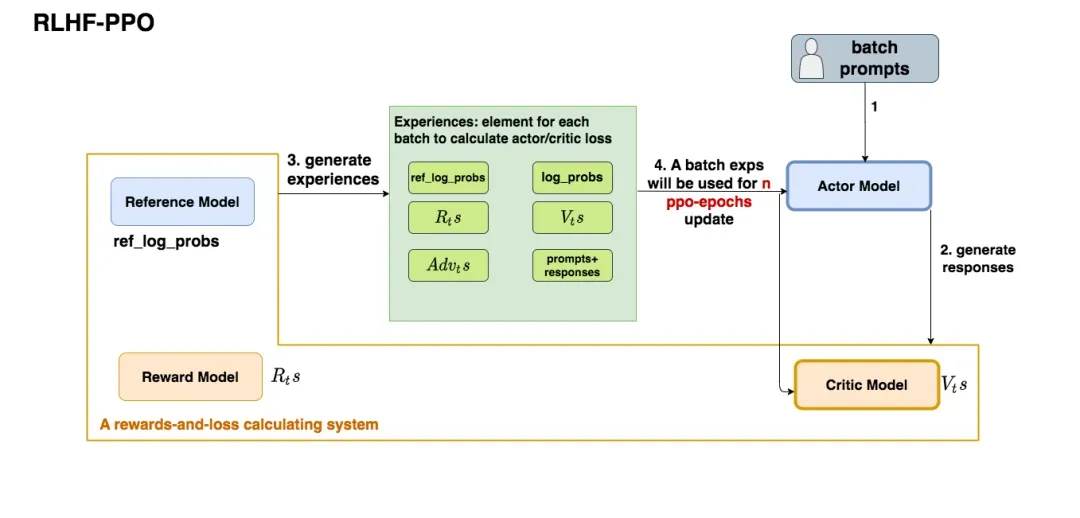
1. 将一个batch的prompts送进Actor语言模型，语言模型产生回答responses；
2. 将prompt + responses送进Critic/Reward/Reference Model，让他们生成用于计算actor/critic loss的数据。按照强化学习的术语，我们将这些数据称为经验；
3. 最后根据这些经验计算出actor/critic loss，然后更新actor和critic model。

其中，我们的actor loss为：

为了区分动作

和优势函数，这里我们将优势函数记为

。而这个loss正是我们的PPO2算法里的优化目标。Critic loss则定义为预估预期收益和实际预期收益的MSE loss。

GRPO算法

铺垫了这么多，终于到我们的核心GRPO算法了。

在上面的PPO算法中，我们通常会引入一个critic model（或者称为value model）来判断每个动作的优劣，从而改进策略。但它的引入也同时带来了两个问题：价值函数估计可能不准确，在LLM的语境里，通常只有一个完整的句子会容易给出一个好坏的判断，而对中间过程生成的token，我们很难给一个准确的奖励值，而价值函数估计不准确则会导致学习策略变差；其次就是模型显存占用高，消耗计算资源大，因为critic model通常和actor model参数量差不多。为了解决这个问题，GRPO算法直接在模型层面删掉了critic model。如下图所示：

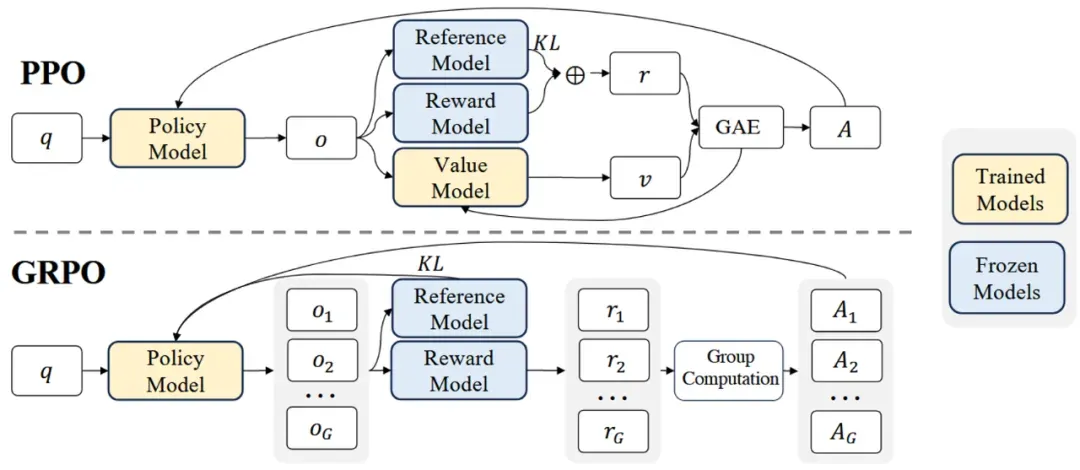
具体来说，GRPO算法的流程如下：

1. 从数据集