数据存储引擎结构详解

介绍

在存储系统的设计中，存储引擎属于底层数据结构，直接决定了存储系统所能够提供的性能和功能。常见存储算法结构涵盖：哈希存储，B 、B+、B*树存储，LSM树存储引擎，R树，倒排索引，矩阵存储，对象与块，图结构存储等等。

哈希存储引擎是哈希表的持久化实现，一般用于键值类型的存储系统。而大多传统关系型数据库使用索引来辅助查找数据，用以加速对数据库数据的访问。考虑到经常需要范围查找，因此其索引一般使用树型结构。譬如MySQL、SQL Server、Oracle中，数据存储与索引的基本结构是B-树和B+树。

主流的NoSQL数据库则使用日志结构合并树(Log-structured Merge Tree)来组织数据。LSM 树存储引擎和B树一样，支持增、删、改、随机读取以及顺序扫描。通过批量转储技术规避磁盘随机写入问题，极大地改善了磁盘的IO性能,被广泛应用于后台存储系统，如Google Big table、Level DB，Facebook Cassandra系统，开源的HBase，Rocks dB等等。

……

一．哈希存储

哈希存储的基本思想是以关键字Key为自变量，通过一定的函数关系(散列函数或哈希函数），计算出对应函数值（哈希地址），以这个值作为数据元素的地址，并将数据元素存入到相应地址的存储单元中。查找时再根据要查找的关键字采用同样的函数计算出哈希地址，然后直接到相应的存储单元中去取要找的数据元素。代表性的使用方包括Redis，Memcache，以及存储系统Bitcask等。

基于内存中的Hash,支持随机的增删改查，读写的时间复杂度O(1)。但无法支持顺序读写(指典型Hash，不包括如Redis的基于跳表的ZSet的其它功能),在不需要有序遍历时，性能最优。

1. 常用哈希函数

构造哈希函数的总的原则是尽可能将关键字集合空间均匀的映射到地址集合空间中，同时尽可能降低冲突发生的概率。

• 除留余数法:H(Key)=key % p (p ≤ m)p最好选择一个小于或等于m(哈希地址集合的个数)的某个最大素数。
• 直接地址法: H(Key) =a * Key + b；“a，b”是常量。
• 数字分析法

比如有一组key1=112233，key2=112633，key3=119033，分析数中间两个数比较波动，其他数不变。那么取key的值就可以是 key1=22,key2=26,key3=90。

• 平方取中法
• 折叠法

比如key=135790，要求key是2位数的散列值。那么将key变为13+57+90=160，然后去掉高位“1”,此时key=60。

2. 冲突处理方法

1) 开放地址法

如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。当程序查找哈希表时，如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，或者遇到一个空的表项。

①.线性探测法

这种方法在解决冲突时，依次探测下一个地址，直到有空的地址后插入，若整个空间都找遍仍然找不到空余的地址，产生溢出。Hi =( H(Key) + di ) % m ( i = 1,2,3,...,k , k ≤ m-1 )

地址增量 di = 1,2,..., m-1, 其中 i 为探测次数

②.二次探测法

地址增量序列为: di= 1^2，-1^2，2^2，-2^2 ，...，q^2，-q^2 (q≤ m/2）

Python字典dict的实现是使用二次探查来解决冲突的。

③.双哈希函数探测法

Hi =( H(Key) + i * RH(Key) ) % m ( i=1,2,3,..., m-1)

H(Key) , RH(Key) 是两个哈希函数，m为哈希表长度。先用第一个哈希函数对关键字计算哈希地址，一旦产生地址冲突，再用第二个函数确定移动的步长因子，最后通过步长因子序列由探测函数寻找空余的哈希地址。H1= (a +b) % m, H2 = (a + 2b) % m, ..., Hm-1= (a+ (m-1)*b) %m

2) 链地址法

将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。

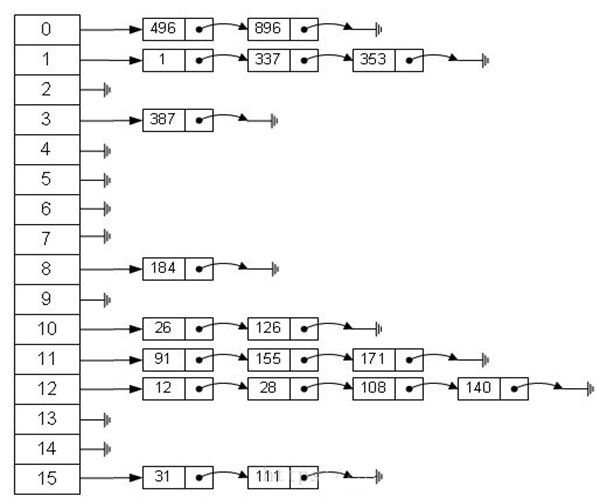
Hash存储示例

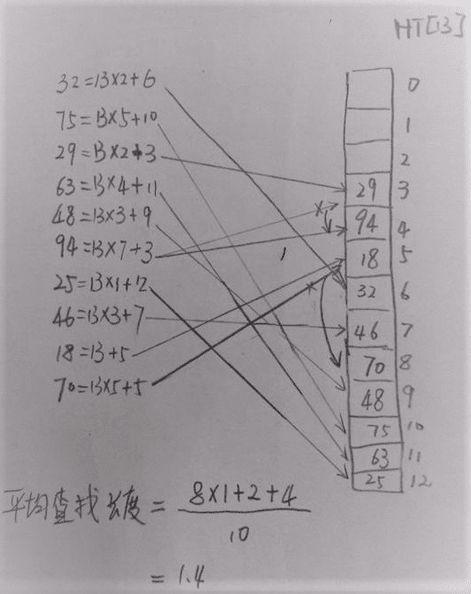
假定一个待散列存储的线性表为(32,75,29,63,48,94,25,46,18,70),散列地址空间为HT[13]，采用除留余数法构造散列函数和线性探测法处理冲突。

二．B 树存储引擎

B树存储引擎是B树的持久化实现，不仅支持单条记录的增、删、读、改操作，还支持顺序扫描（B+树的叶子节点间的指针）。相比哈希存储引擎，B树存储引擎不仅支持随机读取，还支持范围扫描。Mysql的MyISAM和InnoDB支持B-树索引,InnoDB还支持B+树索引，Memory支持Hash。

1. B-树存储

B-树为一种多路平衡搜索树，与红黑树最大的不同在于，B树的结点可以有多个子节点，从几个到几千个。B树与红黑树相似，一棵含n个结点的B树的高度也为O(lgn)，但可能比一棵红黑树的高度小许多，因为它的分支因子比较大。所以B树可在O(logn)时间内，实现各种如插入，删除等动态集合操作。

B-树的规则定义：

1) 定义任意非叶子节点最多可以有M个儿子节点；且M>2；

2) 则根节点的儿子数为：[2，M]；

3) 除根节点为的非叶子节点的儿子书为[M/2，M]；

4) 每个结点存放至少M/2-1(取上整)且至多M -1 个关键字；(至少为2)

5) 非叶子结点的关键字个数 = 指向子节点的指针书 -1；

6) 非叶子节点的关键字：K[1],K[2],K[3],…,K[M-1;且K[i] < K[i +1];

7) 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8) 所有叶子结点位于同一层；

下图是一个M为3的B-树：

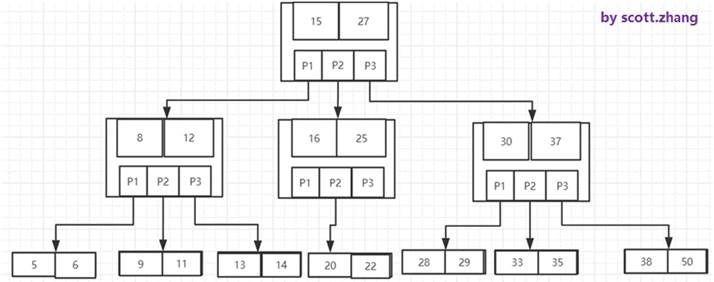
B-树的搜索

从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B-树的特性

关键字集合分布在整颗树中,任何一个关键字出现且只出现在一个结点中；

所有结点都存储数据，搜索有可能在非叶子结点结束；

搜索性能等价于在关键字全集内做一次二分查找,查询时间复杂度不固定，与Key在树中的位置有关，最好为O(1)；

非叶子节点存储了data数据，导致数据量很大的时候，树的层数可能会比较高，随着数据量增加，IO次数的控制不如B+树优秀。

MongoDB 存储结构

MongoDB是聚合型数据库，而B-树恰好Key和data域聚合在一起，所有节点都有Data域，只要找到指定索引就可以进行访问，无疑单次查询平均快于MySql。

MongoDB并不是传统的关系型数据库，而是以Json格式作为存储的NoSQL,目的就是高性能、高可用、易扩展。

2. B+树存储

B树在提高磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题，B+树应运而生。B+树是对B树的一种变形，本质还是多路平衡查找树。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作(或者说效率太低)。RDBMS需要B+树用以减少寻道时间，顺序访问较快。

B+树通常被用于数据库和操作系统的文件系统中。像NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素为自底向上插入。

下图是一棵高度为M=3的B+树

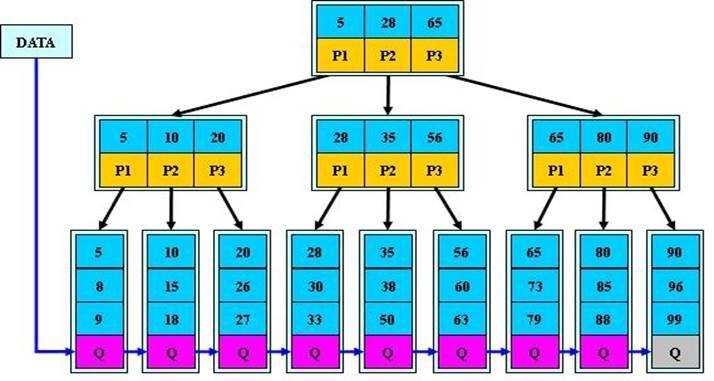
B+树上有两个头指针，一个指向根节点，另一个指向关键字最小的叶子节点，而且所有叶子节点(即数据节点)之间是一种链式环结构。因此可以对B+树进行两种查找运算：一种是对于主键的范围查找和分页查找，另一种是从根节点开始，进行随机查找。

与普通B-树相比，B+树的非叶子节点只有索引，所有关键字都位于叶子节点，这样会使树节点的度比较大，而树的高度就比较低，从而有利于提高查询效率。并且叶子节点上的数据会形成有序链表。

主要优点如下：

• 结构比较扁平，高度低(一般不超过4层)，随机寻道次数少；
• 有n棵子树的结点中含有n个关键字，不用来保存数据，只用来索引。结点中仅含其子树（根结点）中的最大（或最小）关键字。
• 数据存储密度大，且都位于叶子节点，查询稳定，遍历方便；
• 叶子节点存放数值，按照值大小顺序排序，形成有序链表，区间查询转化为顺序读，效率高。且所有叶子节点与根节点的距离相同，因此任何查询效率都很相似。而B树则必须通过中序遍历才支持范围查询。
• 与二叉树不同，B+树的数据更新操作不从根节点开始，而从叶子节点开始，并且在更新过程中树能以比较小的代价实现自平衡。

B+树的缺点：

• 如果写入的数据比较离散，那么寻找写入位置时，子节点有很大可能性不会在内存中，最终产生大量随机写，性能下降。下图说明了这一点。

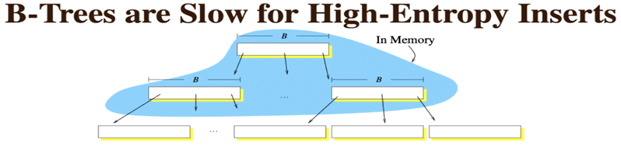
• B+树在查询过程中应该不会慢，但如B+树已运行很长时间，写入了很多数据，随着叶子节点分裂，其对应的块会不再顺序存储而变得分散,可能会导致逻辑上原本连续的数据实际上存放在不同的物理磁盘块位置上，这时执行范围查询也会变成随机读，会导致较高的磁盘IO,效率降低。

譬如：数据更新或者插入完全无序时，如先插入0，后80000，然后200，然后666666，这样跨度很大的数据时，由于不在一个磁盘块中，就需先去查找到这个数据。数据非常离散，就意味着每次查找时，它的叶子节点很可能都不在内存中，此时就会出现性能的瓶颈。并且随机写产生的子树的分裂等，产生很多的磁盘碎片，也是不太友好的一面。

可见B+树在多读少写（相对而言）的情境下比较有优势。当然，可用SSD来获得成倍提升的读写速率，但成本相对较高。

B+树的搜索

与B-树基本相同，区别是B+树只有达到叶子结点才命中(B-树可在非叶子结点命中)，其性能也等价于在关键字全集做一次二分查找。

B+树的特性

非叶子结点相当于是叶子结点的索引(稀疏索引)，叶子结点相当于是存储(关键字)数据的数据层；B+树的叶子结点都是相链的，因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连，所以便于区间查找和搜索。而B-树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻，所以缓存命中性没有B+树好。

比B-树更适合实际应用中操作系统的文件索引和数据库索引

1) 磁盘读写代价更低

B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B树就比B+树多一次盘块查找时间。

2）查询效率更加稳定

由于非叶子结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

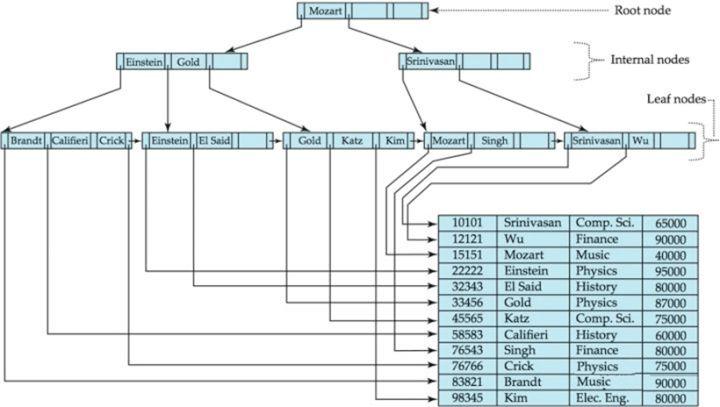
MySQL InnoDB

InnoDB存储引擎中页大小为16KB，一般表的主键类型为INT(占用4字节)或long(8字节)，指针类型也一般为4或8个字节，也就是说一个页(B+树中的一个节点)中大概存储16KB/(8B+8B)=1K个键值(K取估值为10^3)。即一个深度为3的B+树索引可维护10^3 * 10^3 * 10^3=10亿条记录。

在数据库中，B+树的高度一般都在2~4层。MySql的InnoDB存储引擎在设计时是将根节点常驻内存的，也就是说查找某一键值的行记录时最多只需要1~3次磁盘I/O操作。

数据库中的B+树索引可以分为聚集索引(clustered index)和辅助索引(secondary index)。聚集索引的B+树中的叶子节点存放的是整张表的行记录数据。辅助索引与聚集索引的区别在于辅助索引的叶子节点并不包含行记录的全部数据，而是存储相应行数据的聚集索引键，即主键。当通过辅助索引来查询数据时，InnoDB存储引擎会遍历辅助索引找到主键，然后再通过主键在聚集索引中找到完整的行记录数据。

3. B*树存储

B+树的一种变形，在B+树的基础上将索引层以指针连接起来，使搜索取值更加快捷。如下图(M=3)

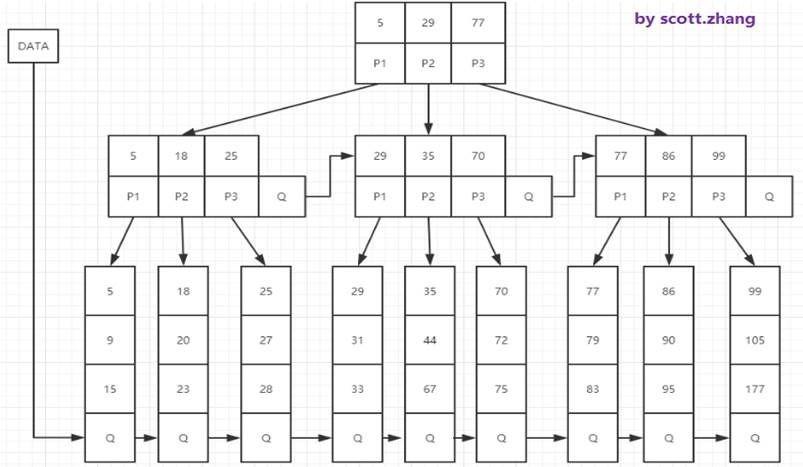
相对B+树的变化，如下：

• B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3代替B+树的1/2，将结点的最低利用率从1/2提高到2/3；
• B+树的分裂:当一个结点满时分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不影响兄弟结点，所以它不需指向兄弟的指针；
• B*树的分裂:当一个结点满时，如它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字(因兄弟结点的关键字范围改变),如兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3数据到新结点,最后在父结点增加新结点的指针.

相对于B+树，B*树分配新结点的概率比B+树要低，空间利用率、查询速率也有所提高。

三．LSM树存储引擎

数据库的数据大多存储在磁盘上，无论是机械硬盘还是固态硬盘(SSD)，对磁盘数据的顺序读写速度都远高于随机读写。大量的随机写，导致B树在数据很大时，出现大量磁盘IO，速度越来越慢，基于B树的索引结构是违背上述磁盘基本特点的—需较多的磁盘随机读写。于是，基于日志结构的新型索引结构方法应运而生,主要思想是将磁盘看作一个大的日志，每次都将新的数据及其索引结构添加到日志的最末端，以实现对磁盘的顺序操作，从而提高索引性能。

对海量存储集群而言，LSM树也是作为B+树的替代方案而产生。当今很多主流DB都使用了LSM树的存储模型，包括LevelDB，HBase，Google BigTable，Cassandra，InfluxDB, RocksDB等。LSM树通过尽可能减少写磁盘次数，实际落地存储的数据按key划分，形成有序的不同文件；结合其“先内存更新后合并落盘”的机制，尽量达到顺序写磁盘，尽可能减少随机写；对于读则需合并磁盘已有历史数据和当前未落盘的驻于内存的更新。LSM树存储支持有序增删改查，写速度大幅提高，但随机读取数据时效率低。

LSM树实际不是一棵树，而是2个或者多个树或类似树的结构的集合。

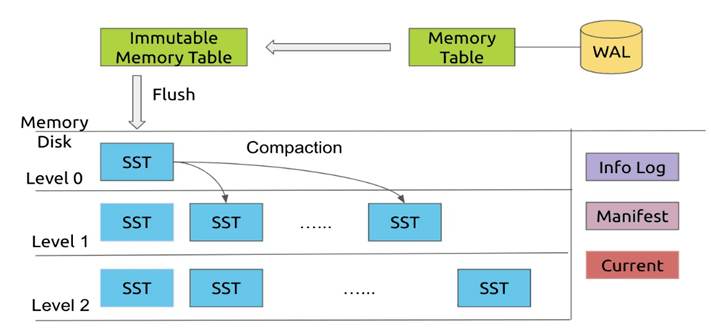
下图为包含2个结构的LSM树

在LSM树中，最低一级即最小的C0树位于内存,而更高级的C1、C2...树都位于磁盘里。数据会先写入内存中的C0树，当它的大小达到一定阈值之后，C0树中的全部或部分数据就会刷入磁盘中的C1树，如下图所示。

由于内存读写速率比外存要快非常多，因此数据写入C0树的效率很高。且数据从内存刷入磁盘时是预排序的，也就是说，LSM树将原本随机写操作转化成了顺序写操作，写性能大幅提升。不过，它的tradeoff就是牺牲了一部分读性能，因为读取时需将内存中数据和磁盘中的数据合并。总体上讲这种权衡还是值得的,因为：

• 可以先读取内存中C0树的缓存数据。内存效率高且根据局部性原理，最近写入的数据命中率也高。
• 写入数据未刷到磁盘时不会占用磁盘的I/O，不会与读取竞争。读取操作就能取得更长的磁盘时间，变相地弥补了读性能差距。

在实际应用中，为防止内存因断电等原因丢失数据，写入内存的数据同时会顺序在磁盘上写日志，类似于预写日志(WAL)，这就是LSM这个词中Log一词的来历。另外，如有多级树，低级的树在达到大小阈值后也会在磁盘中进行合并，如下图所示。

1. Leveldb/Rocksdb

基本描述

1) 对数据，按key划分为若干level，每个level对应若干文件，包括存在于内存中和落盘的。文件内key都有序，同级的各个文件之间一般也有序，level0对应于内存中的数据(0.sst)，后面依次是1、2、3、...的各级文件(默认到level6)。

2) 写时，先写对应内存的最低level的文件，这也是快的一个原因。内存的数据也是被持久化的，达到一定大小后被合并到下一级文件落盘。

3) 落盘后的各级文件也会定期进行排序加合并，合并后数据进入下一层level；这样的写入操作，大多数都是对一个页顺序的写，或者申请新页写，而不再是随机写。

Rocksdb Compact

Compact是个很重要的步骤，下面是rocksdb的compact过程：

Rocksdb的各级文件组织形式：

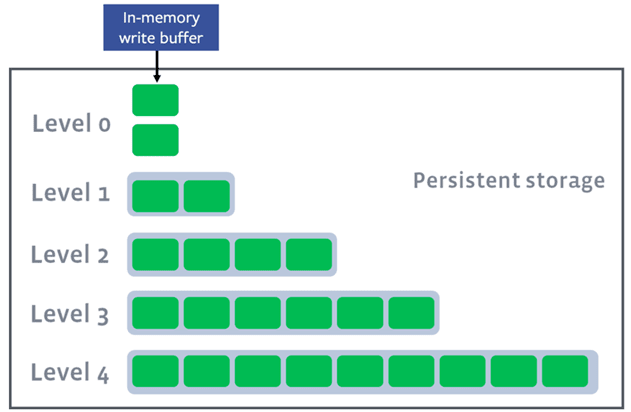
各级的每个文件，内部都按key有序，除了内存对应的level0文件，内部文件之间也是按key有序；这样查找一个key，很方便二分查找。

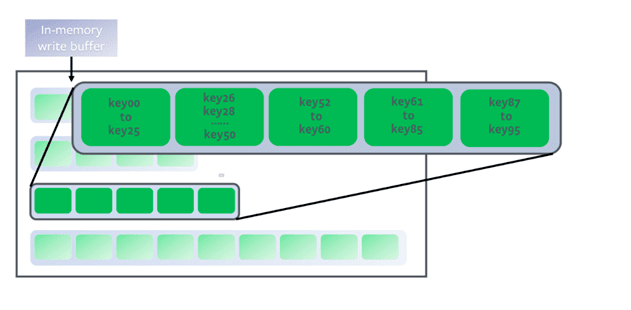
然后，当每一级的数据到达一定阈值时，会触发排序归并，简单说，就是在两个level的文件中，把key有重叠的部分，合并到高层level的文件里

这个在LSM树里叫数据压缩(compact)；

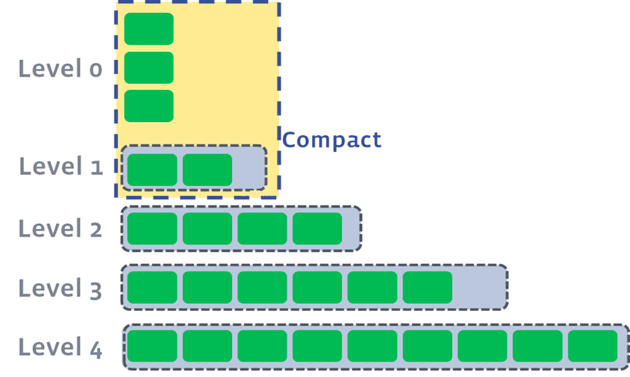
对于Rocksdb，除了内存level0到level1的compact，其他各级之间的compact可以并行；通常设置较小的level0到level1的compact阈值，加快这一层的compact。良好的归并策略的配置，使数据尽可能集中在最高层(90%以上)，而不是中间层，这样有利于compact的速度；另外，对于基于LSM树的读，需要在各级文件中二分查找，磁盘IO也不少，此外还需要关注level0里的对于这个key的操作，比较明显的优化是，通过Bloomfilter略掉肯定不存在该key的文件，减少无谓查找；

2. HBase LSM

说明：本小节需事先了解HBase的读写流程及MemStore。

MemStore作为列族级别的写入和读取缓存，它就是HBase中LSM树的C0层。它未采用树形结构来存储，而是采用了跳表(一种替代自平衡BST二叉排序树的结构)。MemStore Flush的过程，也就是LSM树中C0层刷写到C1层的过程，而LSM中的日志对应到HBase自然就是HLog了。

HBase读写流程简图

HFile就是LSM树中的高层实现。从逻辑上来讲，它是一棵满的3层B+树，从上到下的3层索引分别是Root index block、Intermediate index block和Leaf index block，对应到下面的Data block就是HFile的KeyValue结构。HFile V2索引结构的图示如下：

HFile过多会影响读写性能，因此高层LSM树的合并即对应HFile的合并(Compaction)操作。合并操作又分Minor和Major Compaction，由于Major Compaction涉及整个Region，对磁盘压力很大,因此要尽量避免。

布隆过滤器(Bloom Filter)

是保存在内存中的一种数据结构，可用来验证“某样东西一定不存在或者可能存在”。由一个超长的二进制位数组和一系列的Hash函数组成，二进制位数组初始全部为0，当有元素加入集合时，这个元素会被一系列Hash函数计算映射出一系列的值，所有的值在位数组的偏移量处置为1。如需判断某个元素是否存在于集合中，只需判断该元素被Hash后的值在数组中的值，如果存在为0的则该元素一定不存在；如果全为1则可能存在，这种情况可能有误判。

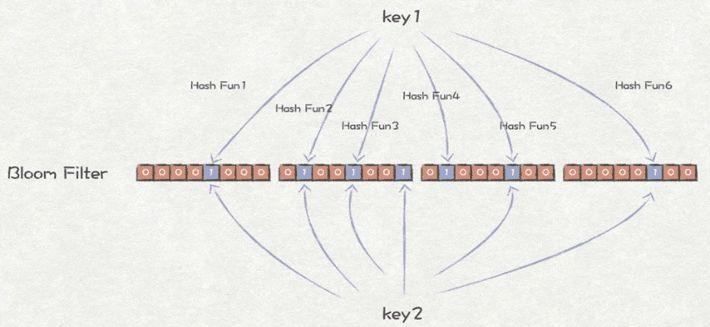
HBase为了提升LSM结构下的随机读性能而引入布隆过滤器(建表语句中可指定)，对应HFile中的Bloom index block，其结构图如下。

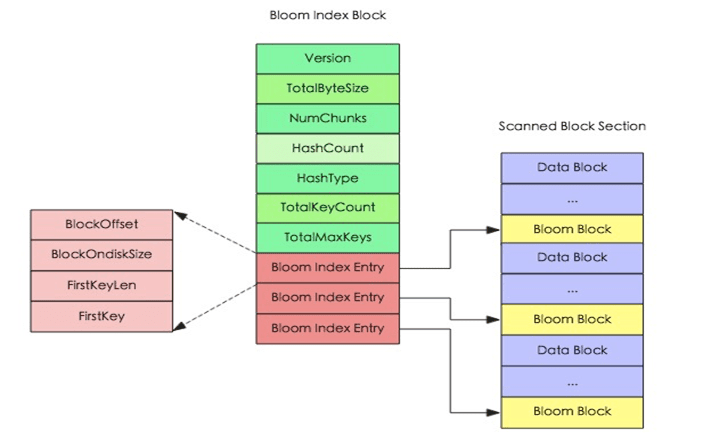
通过布隆过滤器，HBase能以少量的空间代价，换来在读取数据时非常快速地确定是否存在某条数据，效率进一步提升。

LSM-树的这种结构非常有利于数据的快速写入(理论上可接近磁盘顺序写速度），但不利于读,因为理论上读的时候可能需要同时从memtable和所有硬盘上的sstable中查询数据，这样显然会对性能造成较大影响。为解决这个问题，LSM-树采取以下主要相关措施。

• 定期将硬盘上小的sstable合并(Merge或Compaction)成大的sstable，以减少sstable的数量。且平时的数据更新删除操作并不会更新原有的数据文件，只会将更新删除操作加到当前的数据文件末端，只有在sstable合并的时候才会真正将重复的操作或更新去重、合并。
• 对每个sstable使用布隆过滤器,以加速对数据在该sstable的存在性进行判定,从而减少数据的总查询时间。

SSTable(Sorted String Table)

当内存中的MemTable达到一定大小，需将MemTable转储(Dump)到磁盘中生成SSTable文件。由于数据同时存在MemTable和可能多个SSTable中，读取操作需按从旧到新的时间顺序合并SSTable和内存中的MemTable数据。

SSTable 中的数据按主键排序后存放在连续的数据块(Block)中，块之间也有序。接着，存放数据块索引，由每个Block最后一行的主键组成，用于数据查询中的Block定位。接着存放布隆过滤器和表格的Schema信息。最后存放固定大小的Trailer以及Trailer的偏移位置。

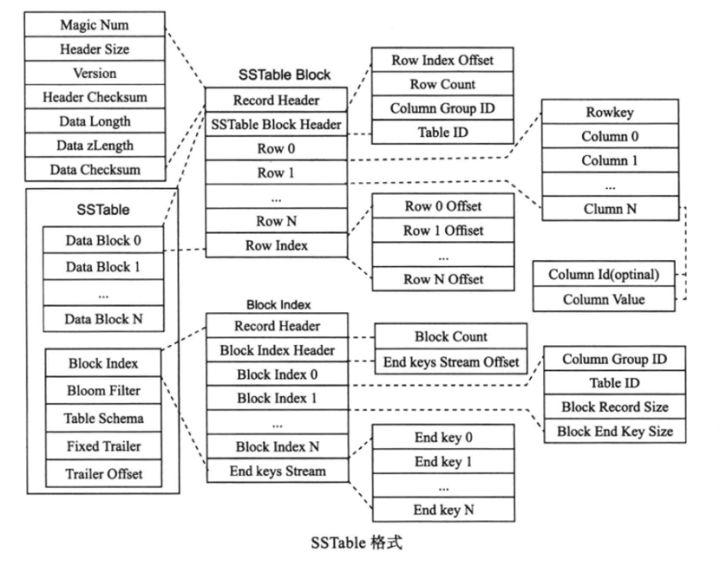
本质上看，SSTable是一个两级索引结构：块索引以及行索引。分为稀疏格式和稠密格式。对于稀疏格式，某些列可能存在也可能不存在，因此每一行只存储包含实际值的列，每一列存储的内容为：<列ID，列值>; 而稠密格式中每一行都需存储所有列，每一列只需存储列值，不需存储列ID，列ID可从表格Schema中获取。

… …

3. 图库ArangoDB LSM

ArangoDB采用RocksDB做底层存储引擎，RocksDB使用LSM-Tree数据结构。

存储的格式非常类似JSON，叫做VelocyPack格式的二进制格式存储。

（1）文档被组织在集合中。

（2）有两种集合：文档（V），边集合（E）

（3）边集合也是以文档形式存储，但包含两个特殊的属性_from和_to，被用来创建在文档和文档之间创建关系

索引类型

· Primary Index，默认索引，建立字段是_key或_id上，一个哈希索引

· Edge Index，默认索引，建立在_from、_to上，哈希索引；不能用于范围查询、排序，弱于OrientDB

· Hash Index，自建

· Skiplist Index，有序索引，

o 用于快速查找具有特定属性值的文档，范围查询以及按索引排序，顺序返回文档。

o 用于查找，范围查询和排序。补全范围查询的缺点。

· Persistent Index，RocksDB的索引。

o 持久性索引是具有持久性的排序索引。当存储或更新文档时，索引条目将写入磁盘。

o 使用持久性索引可能会减少集合加载时间。

· Geo Index，可以在集合中的一个或多个属性上创建其他地理索引。

· Fulltext Index，全文索引

四．R树的存储结构

R树是B树在高维空间的扩展，是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中，也可存在内存中。根据R树的这种数据结构，当需进行一个高维空间查询时，只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足即可。这种方式使得不必遍历所有数据即可获得答案，效率显著提高。

下图是R树的一个简单实例：

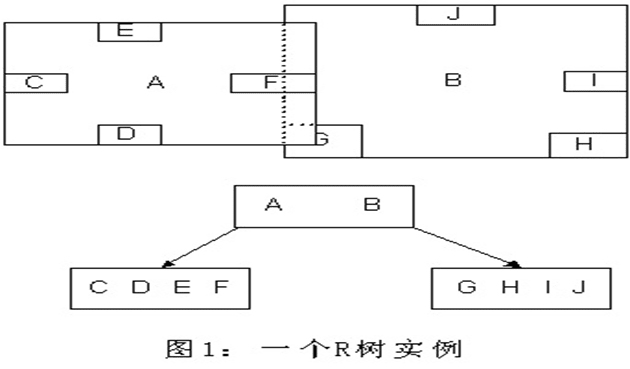
R树运用空间分割理念，采用一种称为MBR(Minimal Bounding Rectangle)的方法，在此译作“最小边界矩形”。从叶子结点开始用矩形将空间框起来，结点越往上，框住的空间就越大，以此对空间进行分割。

以二维空间举例,下图是Guttman论文中的一幅图：

1) 首先假设所有数据都是二维空间下的点，图中仅仅标志了R8区域中的数据，也就是那个shape of data object。别把那一块不规则图形看成一个数据，把它看作是多个数据围成的一个区域。为了实现R树结构，用一个最小边界矩形恰好框住这个不规则区域，这样就构造出了一个区域：R8。R8的特点很明显，就是正好框住所有在此区域中的数据。其他实线包围住的区域，如R9，R10，R12等都是同样道理。这样一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。

2) 下一步操作就是进行高一层次的处理,发现R8，R9，R10三个矩形距离最为靠近，因此就可以用一个更大的矩形R3恰好框住这3个矩形。

3) 同样，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。

用地图和餐厅的例子来解释，就是所有的数据都是餐厅所对应的地点，先把相邻的餐厅划分到同一块区域，划分好所有餐厅之后，再把邻近的区域划分到更大的区域，划分完毕后再次进行更高层次的划分，直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。

然后就可以把这些大大小小的矩形存入R树中。根结点存放的是两个最大的矩形，这两个最大的矩形框住了所有的剩余的矩形，当然也就框住了所有的数据。下一层的结点存放了次大的矩形，这些矩形缩小了范围。每个叶子结点都是存放的最小的矩形，这些矩形中可能包含有n个数据。

查询特定的数据

以餐厅为例，假设查询广州市天河区天河城附近一公里的所有餐厅地址

1) 打开地图(即整个R树)，先选择国内还是国外(根结点);

2) 然后选择华南地区(对应第一层结点)，选择广州市(对应第二层结点);

3) 再选择天河区（对应第三层结点）;

4) 最后选择天河城所在的那个区域(对应叶子结点，存放有最小矩形)，遍历所有在此区域内的结点，看是否满足要求即可。

其实R树的查找规则跟查地图很像，对应下图：

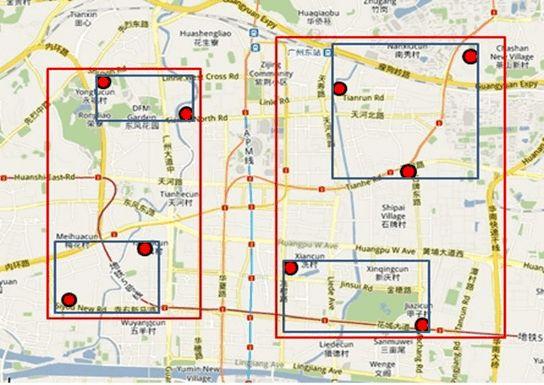
一棵R树满足如下性质：

1) 除非它是根结点之外，所有叶子结点包含有m至M个记录索引(条目)。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。

2) 对于所有在叶子中存储的记录(条目)，I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形(此处所说“矩形”是可扩展到高维空间)。

3) 每一个非叶子结点拥有m至M个孩子结点，除非它是根结点。

4) 对于在非叶子结点上的每一个条目，i是最小的可在空间上完全覆盖这些条目所代表的店的矩形(同性质2)

5) 所有叶子结点都位于同一层，因此R树为平衡树。

说明：

叶子结点的结构，数据形式为: (I, tuple-identifier)，tuple-identifier表示的是一个存放于数据库中的tuple，也就是一条记录，是n维的。I是一个n维空间的矩形，并可恰好框住这个叶子结点中所有记录代表的n维空间中的点。I=(I0,I1,…,In-1)。

R树是一种能够有效进行高维空间搜索的数据结构，已被广泛应用在各种数据库及其相关的应用中。但R树的处理也具局限性，它的最佳应用范围是处理2至6维的数据，更高维的存储会变得非常复杂，这样就不适用。近年来，R树也出现了很多变体，R*树就是其中的一种。这些变体提升了R树的性能，如需更多了解，可以参考相关文献。

应用示例

地理围栏(Geo-fencing)是LBS(Location Based Services)的一种应用，就是用一个虚拟的栅栏围出一个虚拟地理边界，当手机进入、离开某个特定地理区域，或在该区域内活动时，手机可以接收自动通知和警告。譬如，假设地图上有三个商场，当用户进入某个商场的时候，手机自动收到相应商场发送的优惠券push消息。地理围栏应用非常广泛，当今移动互联网主要app如美团、大众点评、手淘等都可看到其应用身影。

五．倒排索引存储

对Mysql来说，采用B+树索引，对Elasticsearch/Lucene来说，是倒排索引。倒排索引(Inverted Index)也叫反向索引，有反向索引必有正向索引。通俗地讲，正向索引是通过key找value，反向索引则是通过value找key。

Elasticsearch是建立在全文搜索引擎库Lucene基础上的搜索引擎，它隐藏了Lucene的复杂性，提供一套简单一致的RESTful API。Elasticsearch的倒排索引其实就是Lucene的倒排索引。

1. Lucene 的倒排索引

倒排索引，通过Term搜索到文档ID。首先想想看，世界上那么多单词，中文、英文、日文、韩文 … 如每次搜索一个单词都要全局遍历一遍，明显不行。于是有了对单词进行排序，像B+树一样可在页里实现二分查找。光排序还不行，单词都放在磁盘，磁盘IO慢的不得了，大量存放内存会导致内存爆了。

下图：通过字典把所有单词都贴在目录里。

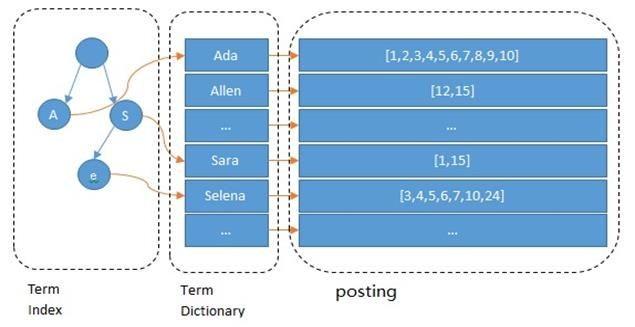
Lucene的倒排索引，增加了最左边的一层「字典树」term index，它不存储所有的单词，只存储单词前缀，通过字典树找到单词所在的块，也就是单词的大概位置，再在块里二分查找，找到对应的单词，再找到单词对应的文档列表。

假设有多个term，如：Carla,Sara,Elin,Ada,Patty,Kate,Selena。找出某个特定term,可通过排序后以二分查找方式，logN次磁盘查找得到目标，但磁盘随机读操作较昂贵(单次Random access约10ms)。所以尽量少的读磁盘，可把一些数据缓存到内存。但term dictionary太大，于是就有了term index.通过trie树来构建index;

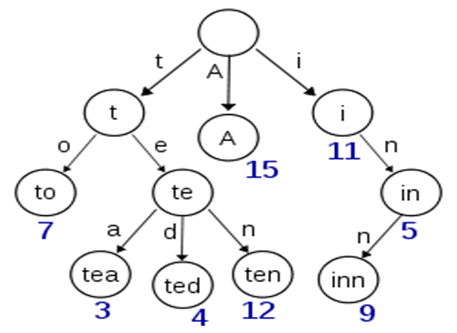
通过term index可快速定位term dictionary的某个offset，从这个位置再往后顺序查找。再加上一些压缩技术(FST)，term index 的尺寸可以只有所有term尺寸的几十分之一，使得用内存缓存整个term index变成可能。

FST Tree

一种有限状态转移机，优点：1）空间占用小。通过对词典中单词前缀和后缀的重复利用，压缩了存储空间；2）查询速度快。O(len(str))的查询时间复杂度。

示例：对“cat”、 “deep”、 “do”、 “dog” 、“dogs”这5个单词进行插入构建FST（必须已排序），得到如下一个有向无环图。

FST压缩率一般在3倍~20倍之间，相对于TreeMap/HashMap的膨胀3倍，内存节省就有9倍到60倍！

2. 与MySQL检索对比

MySQL只有term dictionary，以B-树排序的方式存储在磁盘上。检索一个term需若干次random access磁盘操作。而Lucene在term dictionary的基础上添加了term index来加速检索，以树的形式缓存在内存中。从term index查到对应term dictionary的block位置后，再去磁盘上找term，大大减少磁盘的random access次数。

Term index在内存中是以FST(finite state transducers)的压缩形式保存，其特点是非常节省内存。Term dictionary在磁盘上是以分block的方式保存的，一个block内部利用公共前缀压缩，比如都是Ab开头的单词就可以把Ab省去。这样term dictionary可比B-树更节约空间。

3. 联合索引结构及检索

给定多个查询过滤条件，如”age=18 AND gender=女”就是把两个posting list做一个“与”的合并。对于MySql来说，如果给age和gender两个字段都建立了索引，查询时只会选择其中最selective的来用，然后另一个条件是在遍历行的过程中在内存中计算之后过滤掉。那如何联合使用两个索引呢？两种办法：

• 使用skip list数据结构，同时遍历gender和age的posting list，互相skip；
• 使用bitset数据结构，对gender和age两个filter分别求出 bitset，对两个bitset做AND操作。

PostgreSQL从8.4版本开始支持通过bitmap联合使用两个索引，就是利用bitset数据结构来做的。一些商业的关系型数据库也支持类似联合索引的功能。

ES支持以上两种的联合索引方式，如果查询的filter缓存到了内存中(以bitset形式），那么合并就是两个bitset的AND。如果查询的filter没有缓存，那么就用skip list的方式去遍历两个on disk的posting list。

1) 利用Skip List合并

即使对于排过序的链表，查找还是需要进行通过链表的指针进行遍历，时间复杂度很高依然是O(n)，这个显然不能接受。是否可以像数组那样，通过二分法查找，但由于在内存中的存储的不确定性，不能这么做。但可结合二分法思想，跳表就是链表与二分法的结合。跳表是有序链表。

• 链表从头节点到尾节点都是有序的
• 可以进行跳跃查找(形如二分法），降低时间复杂度

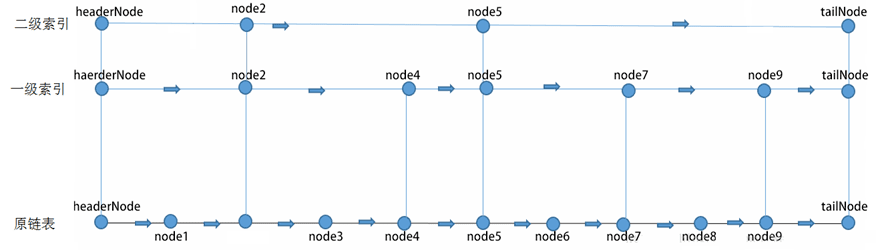
说明：在上图中如要找node6节点

1) 第一次比较headerNode->next[2]的值，即node5的值。显然node5小于node6，所以，下一次应从第2级的node5开始查询，令targetNode=targetNode->next[2];

2) 第二次应该比较node5->next[2]的值，即tailNode的值。tailNode的值是最大的，所以结果是大于，下一次应从第1级的node5开始查询。这里从第2级跳到第1级。但没有改变targetNode。

3) 第三次应该比较node5->next[1]的值，即node7的值。因node7大于node6，所以，下一次应该从第0级的node5开始查询。这里从第1级跳到第0级。也没有改变targetNode。

4) 第四次应该比较node5->next[0]的值，即node6的值。这时相等，结束。如果小于，targetNode往后移，改变targetNode=targetNode->next[0]，如果大于，则没找到，结束。因为这已经是第0级，没法再降了。

考虑到频繁出现的term，如gender里的男或女。如有1百万个文档，那性别为男的posting list里就会有50万个int值。用FOR编码进行压缩可极大减少磁盘占用,对于减少索引尺寸有非常重要的意义。当然MySql B-树里也有类似的posting list，是未经这样压缩的。因为FOR的编码有解压缩成本,利用skip list，除了跳过了遍历的成本，也跳过了解压缩这些压缩过的block的过程，从而节省了CPU。

Frame Of Reference

以下三个步骤组成了Frame Of Reference(FOR)压缩编码技术

Step 1：增量编码

Step 2：分割成块

Lucene每个块是256个文档ID，每个块增量编码后每个元素都不会超过256(1 byte).为方便演示，图中假设每个块是3个文档ID。

Step 3：按需分配空间

对于第一个块 [73, 227, 2]，最大元素是227，需要 8 bits，那给这个块的每个元素，都分配8 bits的空间。但对于第二个块[30,11,29]，最大才30，只需5bits，那给每个元素只分配5bits空间。这一步可说是精打细算，按需分配。

2) 利用bitset合并

Bitset是一种很直观的数据结构，posting list如:[1,3,4,7,10]对应的bitset就是:[1,0,1,1,0,0,1,0,0,1], 每个文档按照文档id排序对应其中的一个bit。Bitset自身就有压缩的特点，其用一个byte就可以代表8个文档。所以100万个文档只需要12.5万个byte。但考虑到文档可能有数十亿之多，在内存里保存bitset仍然是很奢侈的事情。且对于每一个filter都要消耗一个bitset，比如age=18缓存起来的话是一个bitset，18<=age<25是另外一个filter,缓存起来也要一个bitset。所以需要一个数据结构：

• 可以压缩地保存上亿个bit代表对应的文档是否匹配filter；
• 压缩的bitset仍然可以很快地进行AND和OR的逻辑操作。

Roaring Bitmap

Lucene使用这个数据结构，其压缩思路其实很简单,与其保存100个0，占用100个bit，还不如保存0一次，然后声明这个0重复了100遍。

bitmap不管有多少文档，占用的空间都一样。譬如一个数组里面只有两个文档ID：[0, 65535]，表示[1,0,0,0,….(很多个0),…,0,0,1]，需要65536个bit，也就是65536/8=8192 bytes。而用Integer数组只需2*2bytes=4 bytes。可见在文档数量不多时使用Integer数组更节省内存。算一下临界值，无论文档数量多少，bitmap都需要8192bytes，而Integer数组则和文档数量成线性相关，每个文档ID占2bytes，所以8192/2=4096，当文档数量少于4096时用Integer数组，否则用bitmap.

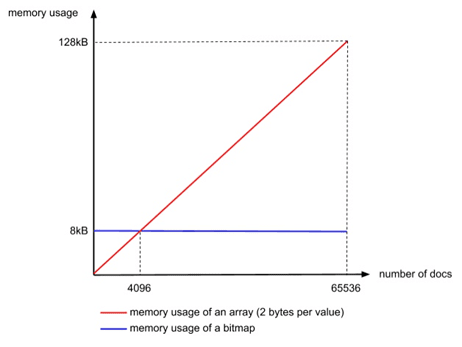
4. 存储文档的减少方式

一种常见的压缩存储时间序列的方式是把多个数据点合并成一行。Opentsdb支持海量数据的一个绝招就是定期把很多行数据合并成一行，这个过程叫compaction。类似的vivdcortext使用MySql存储的时候，也把一分钟的很多数据点合并存储到MySql的一行以减少行数。

ES可实现类似优化，那就是Nested Document。可把一段时间的很多个数据点打包存储到一个父文档里，变成其嵌套的子文档。这样可把数据点公共的维度字段上移到父文档里，而不用在每个子文档里重复存储，从而减少索引的尺寸。

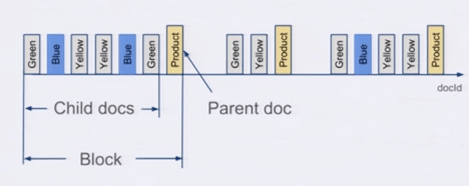
存储时，无论父文档还是子文档，对于Lucene来说都是文档，都会有文档Id。但对于嵌套文档来说，可以保存起子文档和父文档的文档id是连续的，且父文档总是最后一个。有这样一个排序性作为保障，那么有一个所有父文档的posting list就可跟踪所有的父子关系。也可以很容易地在父子文档id之间做转换。把父子关系也理解为一个filter，那么查询检索的时候不过是又AND了另外一个filter而已。

使用了嵌套文档之后，对于term的posting list只需要保存父文档的docid就可，可以比保存所有的数据点的doc id要少很多。如可在一个父文档里塞入50个嵌套文档，那posting list可变成之前的1/50。

… … …

六．对象与块存储

本章节描述，以Ceph 分布式存储系统为参考。

1. 对象存储结构

在文件系统一级提供服务，只是优化了目前的文件系统，采用扁平化方式，弃用了目录树结构，便于共享，高速访问。

对象存储体系结构定义了一个新的、更加智能化的磁盘接口OSD。OSD是与网络连接的设备，包含存储介质，如磁盘或磁带，并具有足够智能可管理本地存储的数据。计算结点直接与OSD通信，访问它存储的数据，不需要文件服务器的介入。对象存储结构提供的性能是目前其它存储结构难以达到的，如ActiveScale对象存储文件系统的带宽可以达到10GB/s。

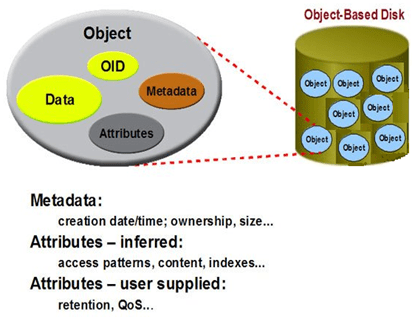
对象存储的结构包括元数据服务器（控制节点MDS）和数据存储服务器（OSD），两者进行数据的存储，还需客服端进行存储的服务访问和使用。

2. 块设备存储

块存储技术的构成基础是最下层的硬件存储设备，可能是机械硬盘也可能是固态硬盘。一个操作系统下可以独立控制多个硬件存储设备，但这些硬件存储设备的工作相对独立，通过操作系统命令看到的也是几个独立的设备文件。通过阵列控制层的设备可以在同一个操作系统下协同控制多个存储设备，让后者在操作系统层被视为同一个存储设备。

典型设备：磁盘阵列，硬盘，虚拟硬盘，这种接口通常以QEMU Driver或者Kernel Module的方式存在，接口需要实现Linux的Block Device的接口或者QEMU提供的Block Driver接口，如Sheepdog，AWS的EBS，阿里云的盘古系统，还有Ceph的RBD（RBD是Ceph面向块存储的接口）。

• 可通过Raid与LVM等手段对数据提供了保护;
• 多块廉价的硬盘组合起来，提高容量;
• 多块磁盘组合出来的逻辑盘，提升读写效率。

Ceph的RBD(RADOS Block Device)使用方式：先创建一个块设备，然后映射块设备到服务器，挂载后即可使用。

七．矩阵的存储结构

说明：本章节以矩阵存储为重心，而非矩阵的运算。

矩阵具有元素数目固定以及元素按下标关系有序排列等特点，所以在使用高级语言编程时，一般是用二维数组来存储矩阵。数据库表数据是行列存储，可视为矩阵的应用形式。矩阵的存储包括完全存储和稀疏存储方式。

1. 常规&特殊矩阵形态

常规矩阵形态

采用二维数组来存储，可按行优先或列优先的形式记录。

特殊矩阵形态

特殊矩阵指的是具有许多相同元素或零元素，并且这些元素的分布有一定规律性的矩阵。这种矩阵如果还使用常规方式来存储，就会产生大量的空间浪费，为了节省存储空间，可以对这类矩阵采用压缩存储，压缩存储的方式是把那些呈现规律性分布的相同元素只分配一个存储空间，对零元素不分配存储空间。

1) 对称矩阵

对于矩阵中的任何一个元素都有aij=aji 1≤i,j≤n这样的矩阵就叫对称矩阵。也就是上三角等于下三角。对于对称矩阵的存储方式是存储上三角或者下三角加对角线，假设一个n阶对称方阵，如果全部存储使用的存储空间是n*n，压缩存储则是n(n+1)/2，对角线元素为n个，除了对角线之外为n*n-n，需要存储的元素(n*n-n)/2，加上对角线上的元素后结果就是n(n+1)/2。假设存储一个n阶对称矩阵，使用sa[n(n+1)/2]来存储，那么sa[k]与ai,j的关系是：

当i>=j时，k= i(i-1)/2+j-1

当i<j 时，k =j(j-1)/2+i-1

2) 三角矩阵

上三角或下三角全为相同元素的矩阵。可用类似于对称矩阵的方式存储，再加上一个位置用来存储上三角或者下三角元素就好。

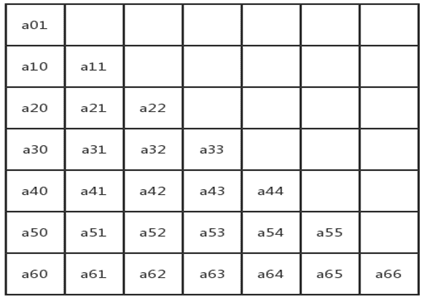
a[i][j]=a[0][0] + (i* (i+1) /2+j) *size;

size为每个数据所占用的存储单元大小。

3) 带状对角矩阵

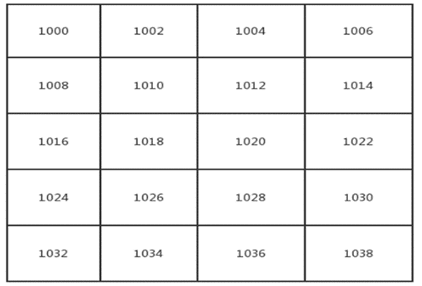
矩阵中所有非0元素集中在主对角线为中心的区域中。下图为3条对角线区域，其他区域的元素都为0。除了第一行和最后一行仅2个非零元素，其余行都是3个非零元素，所以所需的一维空间大小为：3n - 2；

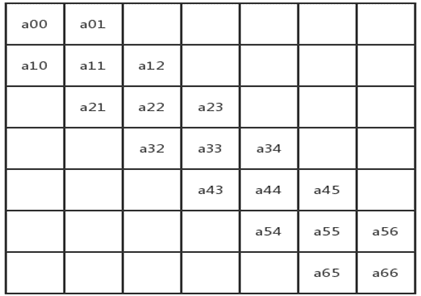
a[i][j]的内存地址=a00首地址+ ((3 * i -1) + (j-i+1)) * size；(size为每个数据所占用的存储单元大小)。比如首地址为1000，每个数据占用2个存储单元，那么a45在内存中的地址=1000+13 * 2=1026；

2. 稀疏矩阵及压缩

由于特殊矩阵中非零元素的分布是有规律的，所以总是可以找到矩阵元素与一维数组下标的对应关系，但还有一种矩阵，矩阵中大多数元素都为0，一般情况下非零元素个数只占矩阵元素总数的5%以下，且元素的分布无规律，这样的矩阵称为稀疏矩阵。

三元组顺序法

如果采用常规方法存储稀疏矩阵，会相当浪费存储空间，因此只存储非零元素。除了存储非零元素的值之外，还需要同时存储非零元素的行、列位置，也就是三元组(i,j,aij)。矩阵元素的存储顺序并没有改变，也是按列的顺序进行存储。

三元组也就是一个矩阵，一个二维数组，每一行三个列，分别为行号、列号、元素值。由于三元组在稀疏矩阵与内存地址间扮演了一个中间人的角色，所以稀疏矩阵进行压缩存储后，便失去了随机存取的特性。

行逻辑链接的顺序表

为了随机访问任意一行的非零元，这种方式需要一个数组指向每一行开始元素(非零元素)的位置。这种方式适合矩阵相乘。

十字链表法

当矩阵中元素非零元个数和位置在操作过程中变化较大时，就不宜采用顺序存储结构来表示三元组的线性表。如在进行加减操作时，会出现非零元变成零元的情况，因此，就适合用十字链表来存储。

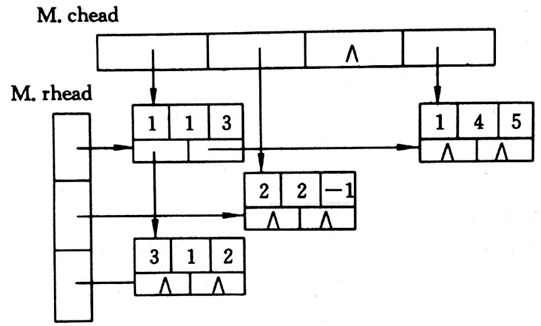
十字链表的结构有五个域，一个数据域存放矩阵元，i、j 域分别存放该非零元所在的行、列。还有right、down域，right指向右边第一个矩阵元的位置，down用来指向下面第一个矩阵元的位置。然后建立两个数组，分别指向每行/列的第一个元素。十字链表在图中也有应用，用来存储图。

八．图结构存储

图通常用来表示和存储具有“多对多”关系的数据，是数据结构中非常重要的一种结构。

1. 邻接矩阵结构

图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

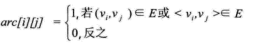
无向图

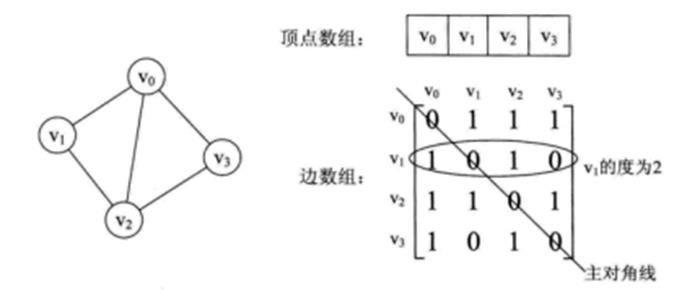
1）基于邻接矩阵容易判断任意两顶点是否有边无边；

2）某个顶点的度就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素和；

3）vi的所有邻接点就是矩阵中第i行元素，如arc[i][j]为1就是邻接点；

n个顶点和e条边的无向网图的创建，时间复杂度为O(n + n2 + e)，其中对邻接矩阵的初始化耗费了O(n2)的时间。

有向图

有向图讲究入度和出度，顶点vi的入度为1，正好是第i列各数之和。顶点vi的出度为2，即第i行的各数之和。

若图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

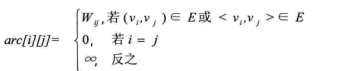
wij表示(vi,vj)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值，也就是一个不可能的极限值。

下面左图是一个有向网图，右图是其邻接矩阵。

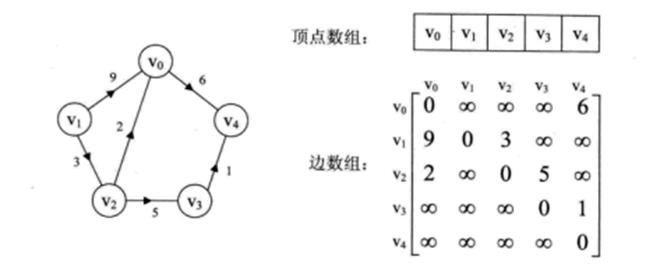
2. 邻接表结构

邻接矩阵是不错的一种图存储结构，但对边数相对顶点较少的图存在对存储空间的极大浪费。因此，找到一种数组与链表相结合的存储方法称为邻接表。邻接表的处理方法：