深度学习中7种最优化算法的可视化与理解

在深度学习中，有很多种优化算法，这些算法需要在极高维度（通常参数有数百万个以上）也即数百万维的空间进行梯度下降，从最开始的初始点开始，寻找最优化的参数，通常这一过程可能会遇到多种的情况，诸如：

1.提前遇到局部最小值从而卡住，再也找不到全局最小值了

2.遇到极为平坦的地方：“平原”，在这里梯度极小，经过多次迭代也无法离开。同理，鞍点也是一样的，在鞍点处，各方向的梯度极小，尽管沿着某一个方向稍微走一下就能离开。

3.“悬崖”，某个方向上参数的梯度可能突然变得奇大无比，在这个地方，梯度可能会造成难以预估的后果，可能让已经收敛的参数突然跑到极远地方去。

为了可视化&更好的理解这些优化算法，我首先拼出了一个很变态的一维函数：

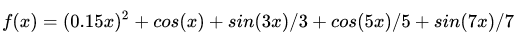
其导数具有很简单的形式

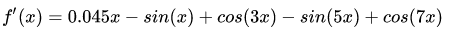
具体长得像：

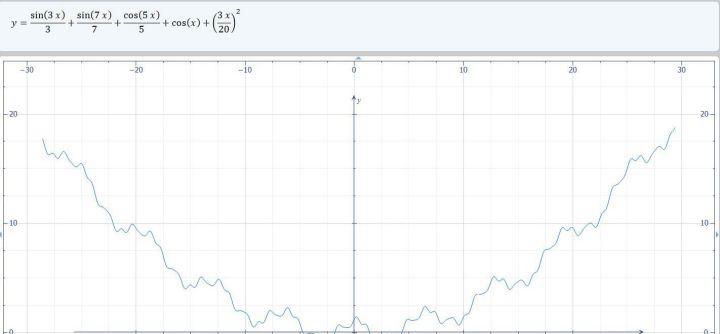
算法1：纯粹的梯度下降法

该算法很简单，表述如下：

首先给出学习率lr，初始x
while True：
x = x - lr*df/dx

根据学习率的不同，可以看到不同的效果。学习率过小，卡在局部极小值，学习率过大，压根不收敛。

梯度下降法

算法2：梯度下降法+动量

算法在纯粹的梯度下降法之上，外加了梯度，从而记录下了历史的梯度情况，从而减轻了卡在局部最小值的危险，在梯度=0的地方仍然会有一定的v剩余，从而在最小值附近摇摆

首先给出学习率lr，动量参数m
初始速度v=0,初始x
while True：
v = m * v - lr * df/dx
x += v

下面可以看图：

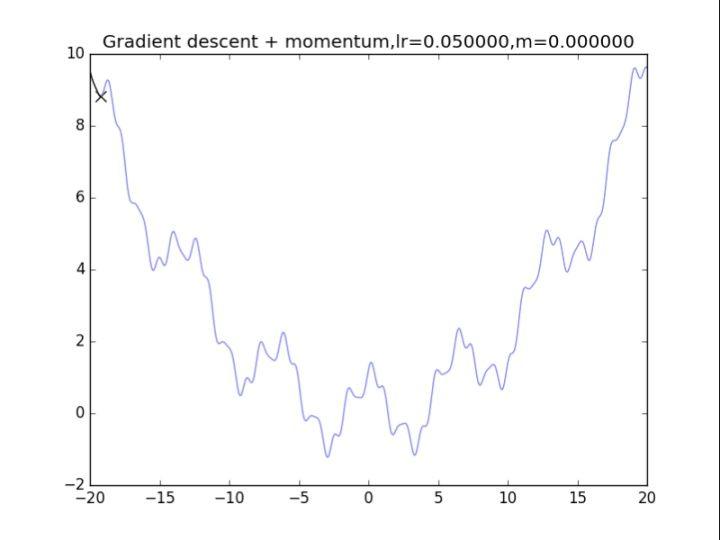梯度下降+动量， lr=0.05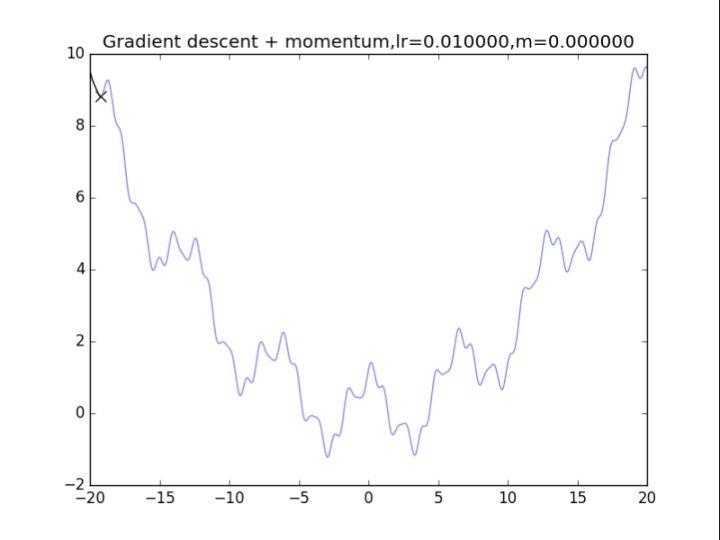梯度下降+动量， lr=0.01梯度下降+动量， lr=0.002

从中我们可以看出：

1. lr越小越稳定，太大了很难收敛到最小值上，但是太小的话收敛就太慢了
2. 动量参数不能太小，0.9以上表现比较好，但是又不能太大，太大了无法停留在最小值处

算法3：AdaGrad算法

AdaGrad算法的思想是累计历史上出现过的梯度（平方），用积累的梯度平方的总和的平方根，去逐元素地缩小现在的梯度。某种意义上是在自行缩小学习率，学习率的缩小与过去出现过的梯度有关。

缺点是：刚开始参数的梯度一般很大，但是算法在一开始就强力地缩小了梯度的大小，也称学习率的过早过量减少。

算法描述：

给出学习率lr，delta=1e-7
累计梯度r=0，初始x
while True：
g = df/dx
r = r + g*g
x = x - lr / (delta+ sqrt(r)) * g

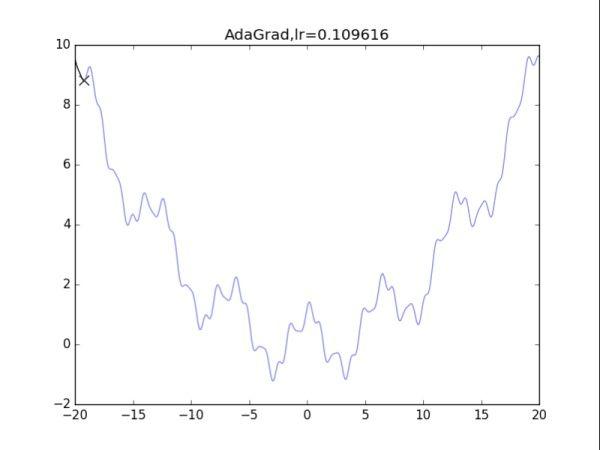
效果并不是很好......

算法4：RMSProp

AdaGrad算法在前期可能会有很大的梯度，自始至终都保留了下来，这会使得后期的学习率过小。RMSProp在这个基础之上，加入了平方梯度的衰减项，只能记录最近一段时间的梯度，在找到碗状区域时能够快速收敛。

算法描述：

给出学习率lr，delta=1e-6，衰减速率p
累计梯度r=0，初始x
while True：
g = df/dx
r = p*r + （1-p）*g*g
x = x - lr / (delta+ sqrt(r)) * g

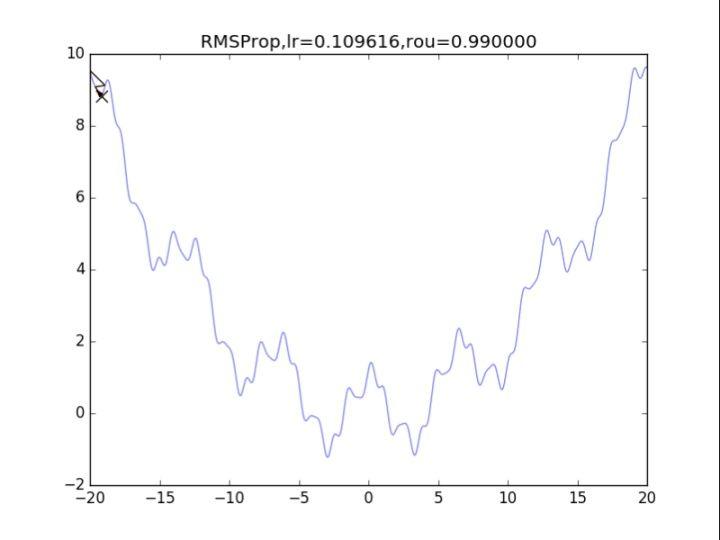RMSProp,p=0.99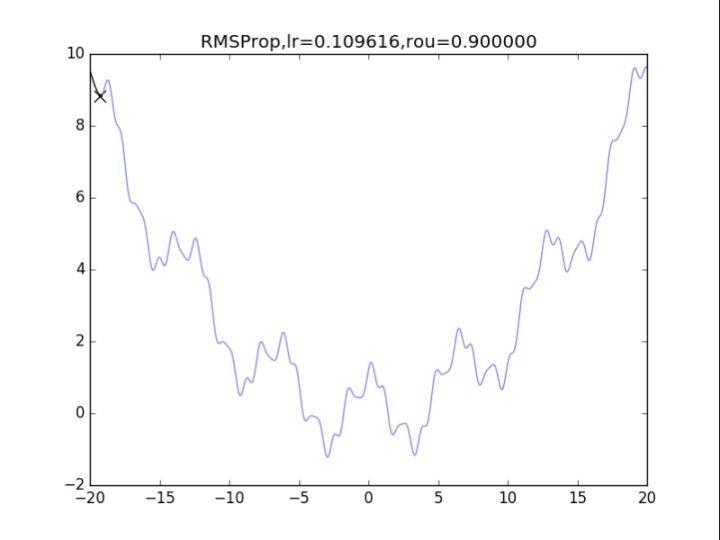RMSProp，p=0.9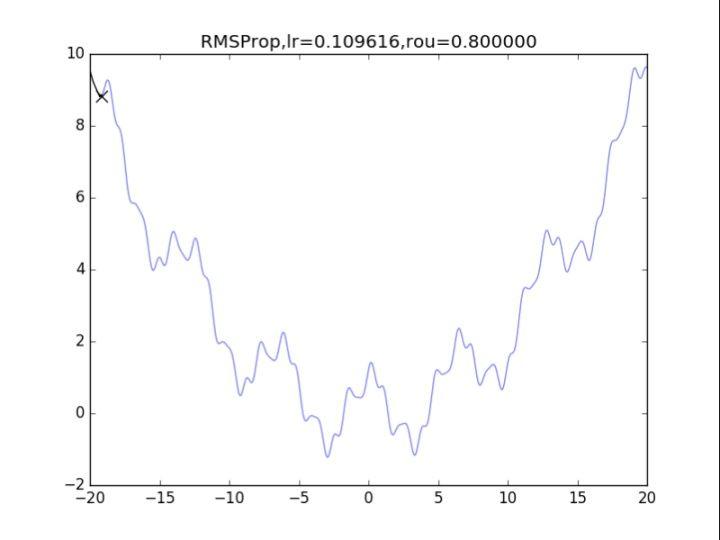RMSProp，p=0.8

衰减速率情况复杂，建议自行调参.......

算法5：Adam算法

Adam算法和之前类似，也是自适应减少学习率的算法，不同的是它更新了一阶矩和二阶矩，用一阶矩有点像有动量的梯度下降，而用二阶矩来降低学习率。

此外还使用了类似于s = s / (1-p1^t)这样的公式，这样的公式在t较为小的时候会成倍增加s，从而让梯度更大，参数跑的更快，迅速接近期望点。而后续t比较大的时候，s = s / (1-p1^t)基本等效于s=s，没什么用。

算法如下：

给出学习率lr，delta=1e-8，衰减速率p1=0.9，p2=0.999
累计梯度r=0，初始x ,一阶矩s=0，二阶矩r=0
时间t = 0
while True：
t += 1
g = df/dx
s = p1*s + (1-p1) *g
r = p2*r +（1-p2）*g*g

s = s / (1-p1^t)
r = r / (1-p2^t)

x = x - lr / (delta+ sqrt(r)) * s

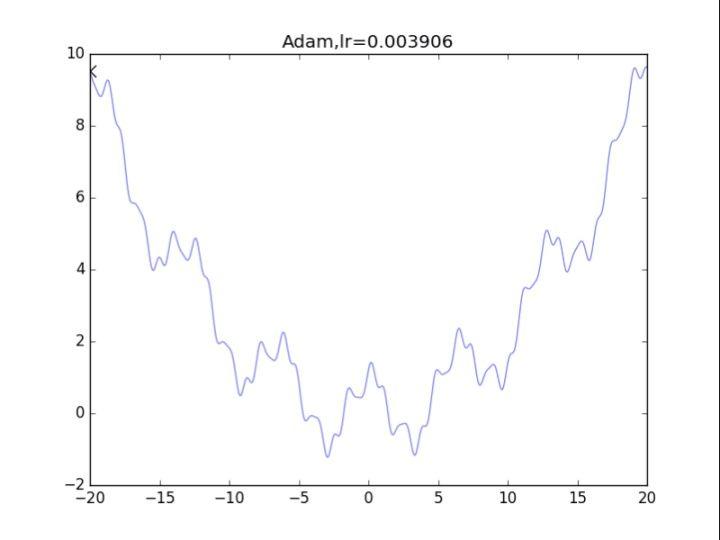Adam算法，鬼一样的表现

是的，你没有看错，这玩意压根不收敛......，表现极差

在算法中仔细研究后才发现，是在t很小的前几步的时候，p2=0.999太大了，导致r = r / (1-p2^t) 中，1-p2^t接近0，r迅速爆炸，百步之内到了inf。后来修改p2=0.9后效果就好的多了

Adam算法，神级表现

最后还是Adam效果最好了 ：)，尽管学习率还是需要相当的调参

算法6：牛顿法

牛顿法是二阶近似方法的一种，其原理类似于将某函数展开到二次方（二次型）项：

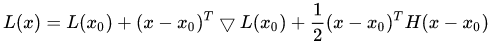
如果幸运的话，这个展开式是一个开口向上的曲面，一步就走到这个曲面的最低点：

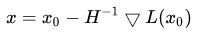
初始x
while True：
g = df(x) # 一阶导数
gg = ddf(x) # 二阶导数
x = x - g/gg # 走到曲面的最低点

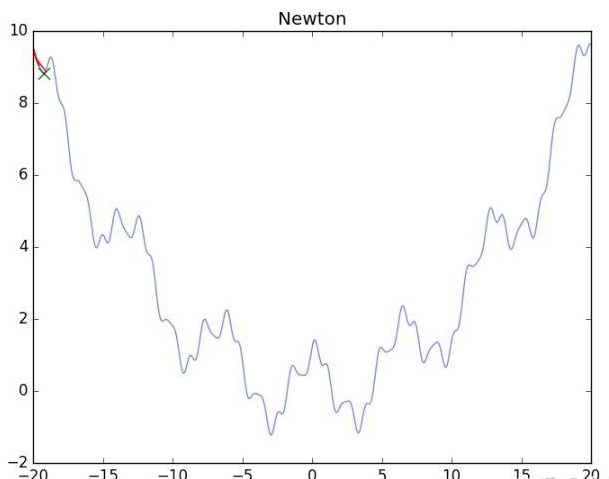可怜的牛顿法，静态图

图片如上，看了真可怜........其实牛顿法要求的是H矩阵正定（一维情况下是二阶导数大于零），在多维中，这样的情况难以满足，大量出现的极小值，悬崖，鞍点都会造成影响，导致无法顺利进行下去，为了更好地进行牛顿法，我们需要正则化它。

算法7：牛顿法+正则化

牛顿法加上正则化可以避免卡在极小值处，其方法也很简单：更新公式改成如下即可

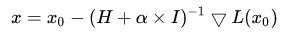
一维的算法如下：

初始x  ，正则化强度alpha
while True：                     
       g = df(x)  # 一阶导数         
       gg = ddf(x)   # 二阶导数         
       x = x - g/（gg+alpha）   # 走到曲面的最低点

效果图：

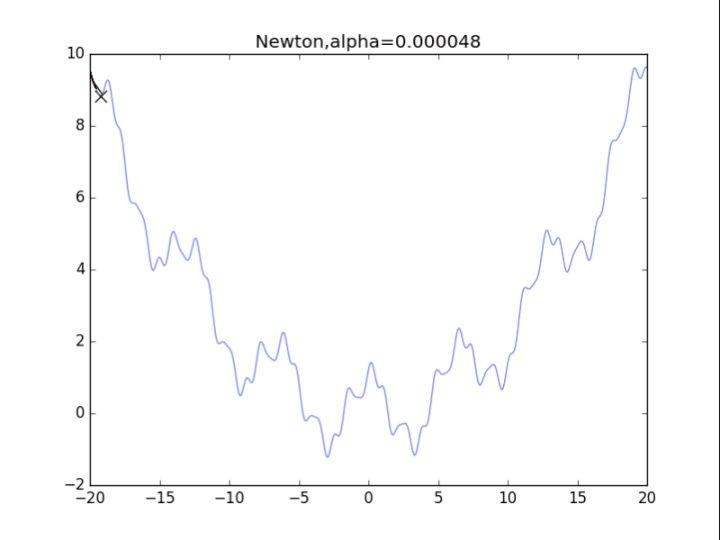牛顿法+正则化

看了真可怜.........二次方法真心在非凸情况很糟糕。此外算法涉及H矩阵的逆，这需要O（n^3）的计算量，非深度学习可用。

代码：