阿里巴巴《Java开发手册（嵩山版）》今日重磅发布！1300个日夜兼程，虚静出内功，嵩山版首次新增前后端规约等内容，全面助力开发者码出规范，码出质量！

8月5日19点，《Java 开发手册》作者孤尽在直播间解读嵩山版更新亮点，从方法论到业务实战教你如何在编程中快速协同，避免踩坑。

《Java开发手册》始于阿里内部规约，在全球Java开发者共同努力下，已成为业界普遍遵循的开发规范，手册涵盖编程规约、异常日志、单元测试、安全规约、MySQL数据库、工程规约、设计规约七大维度。

都说编程是一门艺术，优秀工程师写的代码往往赏心悦目，好代码源于好情怀，好东西自然需要分享出来。回想阿里内部曾组织过一个很有情怀的大型代码分享活动——“向代码致敬，寻找你的第83行代码”，对外以《码出高效》的稿费成立的第83行计划，旨在帮助盲人工程师和山区优秀学生。今天是8月3日，也是《Java开发手册（嵩山版）》发布的日子，在这个数字高度匹配的日子里，我们开怀畅聊一下技术情怀。

工程师是什么样的人？

工程师是一个特殊的群体，在阿里巴巴的占比越来越高，预估即将超过50%，在未来的企业竞争格局中，技术发挥着越来越重要的作用，向技术要红利，向技术要未来。个人以为在技术拓展商业边界之外，需要额外加一条：技术拓展价值边界。这个价值边界的内延是指技术的进无止境，让工程师的人生价值不断升华，不断挖掘自己内心深处的Power，不断提升内心对这份事业的执着感和成就感。价值边界的中延是指打造个人的技术影响力，形成独特的技术品牌，影响到身边的人。价值边界的外延是指有一天你突然发现，不断开拓创新的技术已经影响到世界的每一个角落，甚至是引导一代人的成长。

那工程师又是什么样的用户画像？闷骚、男性为主、理性思维、人不狠，话不多、更愿意人机互动、自我中心感偏强烈、对代码有着强烈的自尊感、对于别人的代码偶尔会有着发自内心的鄙视感。入职一家新公司并在电脑面前看别人的代码时，大部分人的第一反应：脏、乱、差，很少有人觉得别人的代码写得妙笔生花，通俗易懂。所以重构往往是技术同学的情结，重构的理由能够讲得天花乱坠，重构的频率随着人员频繁更替越来越高。

如何让工程师们成为更好的自己，成了一个绕不开的话题。在阿里巴巴，把人的文化想象成一个同心圆，对于每个人的最内核价值要求是公司的六脉神剑，次外层是人才观，即：乐观、皮实、聪明、自省，其中我最看重的是聪明和自省。聪明指的是打开自己的能力和阅读别人的能力，计算机专业的毕业生智商自然不低，甚至是天赋异禀，但是恃才傲物，不打开自己，不共享优秀的经验和代码，无法使个人的优秀产生集体化学反应；不阅读别人，无法高效地与他人合作，从而影响到组织的效能。至于自省，如果你觉得肯定、一定、绝对是对的，一般是错误的开始，懂得自省，不是否定自己，而是下一个成功的开始。单纯的价值观和人才观不足以驱动工程师这个群体更好地进步与创新，那么我们需要一种更立体的技术情怀来驱动个体、团队、组织继续前行。

技术情怀是什么？

情怀是近年的热词，可是谁也没有清晰地解释过情怀是什么。个人认为情怀是一种难舍难分的感情，即使风雨兼程，依然故我，坚信雨后彩虹会更美。退一步说，即使没有彩虹出现，享受雨后带着泥土芬芳的清新空气，享受追求梦想的历程就好，用武侠文化来说，情怀是行侠仗义之于江湖，快意潇洒之于恩仇，大江南北，侠之大者，为国为民；侠之小者，为红颜，为知己。

技术情怀是一种匠心，是一个偏务虚的词语，工程师是偏向于数据驱动的群体，希望能够用数据来量化定义，能够明确符合什么特质，达到什么程度的人，才是具有技术情怀的。我尝试从三个维度来解读一下技术情怀，总结成三个关键词：热爱、思考、卓越。热爱是一种源动力，思考是一个过程，卓越是一个结果。如果要给这三个词加一个定语，以使技术情怀更加立体、清晰地被解读，那这个定语就是：奉献式的热爱，主动式的思考，极致式的卓越。对于工程师来说，即使他热爱架构设计，热爱写代码，并且能写好代码，但是他不奉献不分享，同样会使技术视野变得很窄。思考如果是被动式的，是主管、业务方叫你思考，那么这种思考有时候往往是缺乏想象力和创新力的。卓越如果有顶点，那么容易固步自封。

奉献式的热爱

热爱，是一种兴趣，一种爱好。奉献，这种兴趣和爱好，能够普惠他人，造福社会，有着吃亏是福的豪气。有时候技术总是孤独的，我写了几千页的总结，这些总结都是深夜、周末、假期中，一个人走过来的。有时候被挑战、被否定、自己难受的时候，蹲下来，抱抱委屈的自己，便能有所缓和，继续自己的追求和热情。因此，有人说我的花名是孤独的尽头，简称孤尽（真正释义是风清扬的“独孤九剑，破尽天下武功”的说法）。

人们通常有两个常见的毛病：患得，患失。而热爱一件事情，除了执着，不会在得失上顾虑太多。很多人觉得《Java开发手册》是阿里巴巴KPI的产物，我并不反对KPI，但内心的热爱，与这些暂时的得失又有什么关系呢？马总说除了智商，情商，还有一种叫爱商——爱家人、爱恋人、爱朋友。扩展一下，热爱自己的事业，并且这种热爱不会因为短期的质疑、否定而放弃。

经常有人问我，编写和推广《Java开发手册》如此费心费力，什么样的信念让我如此执着？陆川的电影《可可西里》印象非常深刻，很多事情因为坚持而有希望，而不是有希望才坚持。为可可西里自然保护区的设立做过巨大贡献的索南达杰，毕生都献给了藏羚羊的保护，放弃了很多，甚至献出了他宝贵的生命，人因为信念而坚持体现出人类的伟大。忽悠是把我不相信的东西说给大家听，但是信念是把相信的东西用行动传递给大家。手册的愿景是码出高效，码出质量，码出未来，帮助到更多的人，推进世界的规约文化进步，能够觉得协同开发是一件幸福的事情，开发是一件有创造力的事情，开发是一件能够改变世界的事情，而不是为了琐碎规则的意见相左而消耗巨大的能量，影响了算法效率和架构设计的优雅性。

主动式的思考

很多人以为，《Java开发手册》只是信息收集整理后的文档而已，代码规约的70%内容完全出自平时个人的总结和技术提炼。冰冻三尺，绝非一日之寒，展示给大家的小板凳，已经是第n只，并且还在不断地改进中，不断地自我思考中，去提升自己对知识的认知层次和抽象水平。

我习惯去做摘记，从入职第一天开始，总共沉淀了近2300页的笔记，分为四个文档，搜集、整理、专题、哲学。知识快速进入搜集区，包括听到的、看到的、疑惑的，不断地去思考，不断地去清理、复核、总结之后，沉淀于整理区，这是点维度的总结。把这些点的知识串成一个专题是线维度的总结。而最后的知识上升到哲学方法论级别，是面维度的总结。有一些至今没有搞清楚的知识点，在搜集区已经沉淀了多年，依然会不断地去Review一下。所以，我对于知识的记忆非常清晰，因为那是不断进行主动式思考的结果。经过一段时间的整理之后，形成某个知识体系，比如，高并发处理、Docker技巧、函数式编程等，会形成一个新的文档——体系化总结。而最后的思考就是把知识体系抽象成哲学思维，任何问题上升到高层抽象就是哲学知识。主动沉淀、主动思考、主动提炼，才能使我们的技术境界不断升华。

极致式的卓越

对客户我们要求Stay humble，对技术我们提倡Keep ambitious，敢于卓越，敢于极致。极致与卓越，似乎是一个意思，即出类拔萃，超出期望。极致式的卓越，是把卓越再往前提升一个等级。如果一个人处在一个无人可以比拟的高度上，那么他要学会自我驱动，持续进步，不但卓越，还要追求个人内心极致的追求。“自信人生二百年，会当水击三千里”，坚持成就更好的公司，更好的未来，自然会成就更好的自己。

对于写代码有极致追求的人，总会不断地去Review自己的代码，并且和同事进行Code Review，极致式地追求代码的清晰、可读性。追求到极致，就是能够有9行完成的代码，坚决不写10行；能够写出50ms的接口，坚决不写成100ms。常常Review一下自己的代码是否符合开闭原则，是否有利于维护和扩展。

希望《Java开发手册（嵩山版）》是陪伴大家的床头书，地铁中翻一下神清气爽的工具书，内功修炼的武功秘籍。因为卓越，所以经典，只有这样百尺竿头，才能更进一步。有人曾经留言说到这个手册与星爷的电影一样经典，我真的非常感动。追求卓越，追求极致式的卓越，是技术情怀的核心。

《码出高效》的写作是在深度拷打我的情怀和使命感，中间的痛楚与质疑，让自己的内心一度怀疑写书是一件错误的事情，忽略了时间和空间，忽略了家人，忽略了身体。如果一定要给技术情怀加一个续的话，那么我希望大家响应毛爷爷1952年的号召：发展体育运动，增强人民体质。把知识传播给大家，帮助到一代程序员的成长，需要奉献、需要不断地精进、需要不断地深度思考。

嵩山归来

天龙八部给我最深的印象是扫地僧从容淡定地在弹指之间制服两大绝世高手，功力之高深莫测，清幽现云山，虚静出内功，是一种武学情怀。《Java开发手册》从华山到泰山，一路星夜兼程，今天的嵩山版经过不断地精进与苦练，已经日臻完美，它的内功提升之处在于：

• 第一、增加前后端规约。打通前后端的任督二脉，形成前后端协作开发的共识。
• 第二、重画分层图例。新图更加突出分层的清晰度，并且去掉图中有歧义的向上箭头。
• 第三、修正BigDecimal的equals错误。3.0与3.00在我们的常规认知里是相等的，但是equals比较的结果由于考虑到精度因素，所以返回为false。
• 第四、修正泰山版的部分文字描述错误。

解读1：

8月3日，这个在我等码农心中具有一定纪念意义的日子里，《Java开发手册》发布了嵩山版。每次发布我都特别期待，因为总能找到一些程序员不得不重视的“血淋淋的巨坑”。比如这次，嵩山版中新增的模块——前后端规约，其中一条禁止服务端在超大整数下使用Long类型作为返回。

这个问题，我在实际开发中遇到过，所以印象也特别深。如果在业务初期没有评估到这一点，将订单ID这类关键信息，按照Long类型返回给前端，可能会在业务中后期高速发展阶段，突然暴雷，导致严重的业务故障。期望大家能够重视。

这条规约给出了直接明确的避坑指导，但要充分理解背后的原理，知其所以然，还有很多点要思考。首先，我们来看几个问题，如果能说出所有问题的细节，就可直接跳过了，否则下文还是值得一看的：

• 一问：JS的Number类型能安全表达的最大整型数值是多少？为什么（注意要求更严，是安全表达）？
• 二问：在Long取值范围内，2的指数次整数转换为JS的Number类型，不会有精度丢失，但能放心使用么？
• 三问：我们一般都知道十进制数转二进制浮点数有可能会出现精度丢失，但精度丢失具体怎么发生的？
• 四问：如果不幸中招，服务端正在使用Long类型作为大整数的返回，有哪些办法解决？

基础回顾

在解答上面这些问题前，先介绍本文涉及到的重要基础：IEEE754浮点数标准。如果大家对IEEE754的细节烂熟于心的话，可以跳过本段内容，直接看下一段，问题解答部分。

当前业界流行的浮点数标准是IEEE754，该标准规定了4种浮点数类型:单精度、双精度、延伸单精度、延伸双精度。前两种类型是最常用的。我们单介绍一下双精度，掌握双精度，自然就了解了单精度（而且上述问题场景也是涉及双精度）。

双精度分配了8个字节，总共64位，从左至右划分是1位符号、11位指数、52位有效数字。如下图所示，以0.7为例，展示了双精度浮点数的存储方式。

存储位分配

1）符号位：在最高二进制位上分配1位表示浮点数的符号，0表示正数，1表示负数。

2）指数：也叫阶码位。

在符号位右侧分配11位用来存储指数，IEEE754标准规定阶码位存储的是指数对应的移码，而不是指数的原码或补码。根据计算机组成原理中对移码的定义可知，移码是将一个真值在数轴上正向平移一个偏移量之后得到的，即[x]移=x+2^(n-1)（n为x的二进制位数，含符号位）。移码的几何意义是把真值映射到一个正数域，其特点是可以直观地反映两个真值的大小，即移码大的真值也大。基于这个特点，对计算机来说用移码比较两个真值的大小非常简单，只要高位对齐后逐个比较即可，不用考虑负号的问题，这也是阶码会采用移码表示的原因所在。

由于阶码实际存储的是指数的移码，所以指数与阶码之间的换算关系就是指数与它的移码之间的换算关系。假设指数的真值为e，阶码为E ，则有 E = e + (2 ^ (n-1) - 1)，其中 2 ^ (n-1) - 1 是IEEE754 标准规定的偏移量。则双精度下，偏移量为1023，11位二进制取值范围为[0，2047]，因为全0是机器零、全1是无穷大都被当做特殊值处理，所以E的取值范围为[1,2046]，减去偏移量，可得e的取值范围为[-1022,1023] 。

3）有效数字：也叫尾数位。最右侧分配连续的52位用来存储有效数字，IEEE754标准规定尾数以原码表示。

浮点数和十进制之间的转换

在实际实现中，浮点数和十进制之间的转换规则有3种情况：

1 规格化

指数位不是全零，且不是全1时，有效数字最高位前默认增加1，不占用任何比特位。那么，转十进制计算公式为：

(-1)^s*(1+m/2^52)*2^(E-1023)

其中s为符号，m为尾数，E为阶码。比如上图中的0.7 :

1）符号位：是0，代表正数。

2）指数位：01111111110，转换为十进制，得阶码E为1022，则真值e=1022-1023=-1。

3）有效数字：

0110011001100110011001100110011001100110011001100110

转换为十进制，尾数m为：1801439850948198。

4）计算结果：

(1+1801439850948198/2^52)*(2^-1) =0.6999999999999999555910790149937383830547332763671875

经过显示优化算法后(在后文中详述)，为0.7。

2 非规格化

指数位是全零时，有效数字最高位前默认为0。那么，转十进制计算公式：

(-1)^s*（0+m/2^52)*2^(-1022)

注意，指数位是-1022，而不是-1023，这是为了平滑有效数字最高位前没有1。比如非规格最小正值为：

0x0.00000000000012^-1022=2^-52 2^-1022 = 4.9*10^-324

3 特殊值

指数全为1，有效数字全为0时，代表无穷大；有效数字不为0时，代表NaN（不是数字）。

问题解答

1 JS的Number类型能安全表达的最大整型数值是多少？为什么？

规约中已经指出：

在Long类型能表示的最大值是2的63次方-1，在取值范围之内，超过2的53次方(9007199254740992)的数值转化为JS的Number时，有些数值会有精度损失。

“2的53次方”这个限制是怎么来的呢？如果看懂上文IEEE754基础回顾，不难得出：在浮点数规格化下，双精度浮点数的有效数字有52位，加上有效数字最高位前默认为1，共53位，所以JS的Number能保障无精度损失表达的最大整数是2的53次方。

而这里的题问是：“能安全表达的最大整型”，安全表达的要求，除了能准确表达，还有正确比较。2^53=9007199254740992，实际上，

9007199254740992+1 == 9007199254740992

的比较结果为true。如下图所示：

这个测试结果足以说明2^53不是一个安全整数，因为它不能唯一确定一个自然整数，实际上9007199254740992、9007199254740993，都对应这个值。因此这个问题的答案是：2^53-1。

2 在Long取值范围内，2的指数次整数转换为JS的Number类型，不会有精度丢失，但能放心使用么？

规约中指出：

在Long取值范围内，任何2的指数次整数都是绝对不会存在精度损失的，所以说精度损失是一个概率问题。若浮点数尾数位与指数位空间不限，则可以精确表示任何整数。

后半句，我们就不说了，因为绝对没毛病，空间不限，不仅是任何整数可以精确表示，无理数我们也可以挑战一下。我们重点看前半句，根据本文前面所述基础回顾，双精度浮点数的指数取值范围为[-1022,1023]，而指数是以2为底数。另外，双精度浮点数的取值范围，比Long大，所以，理论上Long型变量中2的指数次整数一定可以准确转换为JS的umber类型。但在JS中，实际情况，却是下面这样：

2的55次方的准确计算结果是：36028797018963968，而从上图可看到，JS的计算结果是：36028797018963970。而且直接输入36028797018963968，控制台显示结果是36028797018963970。

这个测试结果，已经对本问题给出答案。为了确保程序准确，本文建议，在整数场景下，对于JS的Number类型使用，严格限制在2^53-1以内，最好还是信规约的，直接使用String类型。

为什么会出现上面的测试现象呢？

实际上，我们在程序中输入一个浮点数a，在输出得到a'，会经历以下过程：

1）输入时：按照IEEE754规则，将a存储。这个过程很有可能会发生精度损失。

2）输出时：按照IEEE754规则，计算a对应的值。根据计算结果，寻找一个最短的十进制数a'，且要保障a'不会和a隔壁浮点数的范围冲突。a隔壁浮点数是什么意思呢？由于存储位数是限定的，浮点数其实是一个离散的集合，两个紧邻的浮点数之间，还存在着无数的自然数字，无法表达。假设有f1、f2、f3三个升序浮点数，且它们之间的距离，不可能在拉近。则在这三个浮点数之间，按照范围来划分自然数。而浮点数输出的过程，就是在自己范围中找一个最适合的自然数，作为输出。如何找到最合适的自然数，这是一个比较复杂的浮点数输出算法，大家感兴趣的，可参考相关论文[1]。

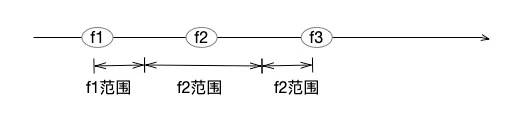
所以，36028797018963968和36028797018963970这两个自然数，对应到计算机浮点数来说，其实是同一个存储结果，双精度浮点数无法区分它们，最终呈现哪一个十进制数，就看浮点数的输出算法了。下图这个例子可以说明这两个数字在浮点数中是相等的。另外，大家可以想想输入0.7,输出是0.7的问题，浮点数是无法精确存储0.7，输出却能够精确，也是因为有浮点数输出算法控制（特别注意，这个输出算法无法保证所有情况下，输入等于输出，它只是尽力确保输出符合正常的认知）。

扩展

JS的Number类型既用来做整数计算、也用来做浮点数计算。其转换为String输出的规则也会影响我们使用，具体规则如下：

上面是一段典型的又臭又长但逻辑很严谨的描述，我总结了一个不是很严谨，但好理解的说法，大家可以参考一下：

除了小数点前的数字位数(不算开始的0)少于22位，且绝对值大于等于1e-6的情况，其余都用科学计数法格式化输出。举例：

3 我们一般都知道十进制数转二进制浮点数有可能会出现精度丢失，精度丢失怎么发生的？

通过前面IEEE754分析，我们知道十进制数存储到计算机，需要转换为二进制。有两种情况，会导致转换后精度损失：

1）转换结果是无限循环数或无理数

比如0.1转换成二进制为：

0.0001 10011001100110011001100110011...

其中0011在循环。将0.1转换为双精度浮点数二进制存储为：

0 01111111011 1001100110011001100110011001100110011001100110011001

按照本文前面所述基础回顾中的计算公式 (-1)^s(1+m/2^52)2^(E-1023)计算，可得转换回十进制为：0.09999999999999999。这里可以看出，浮点数有时是无法精确表达一个自然数，这个和十进制中1/3 =0.333333333333333...是一个道理。

2）转换结果长度，超过有效数字位数，超过部分会被舍弃

IEEE754默认是舍入到最近的值，如果“舍”和“入”一样接近，那么取结果为偶数的选择。

另外，在浮点数计算过程中，也可能引起精度丢失。比如，浮点数加减运算执行步骤分为：

零值检测 -> 对阶操作 -> 尾数求和 -> 结果规格化 -> 结果舍入

其中对阶和规格化都有可能造成精度损失：

• 对阶：是通过尾数右移（左移会导致高位被移出，误差更大，所以只能是右移），将小指数改成大指数，达到指数阶码对齐的效果，而右移出的位，会作为保护位暂存，在结果舍入中处理，这一步有可能导致精度丢失。
• 规格化：是为了保障计算结果的尾数最高位是1，视情况有可能会出现右规，即将尾数右移，从而导致精度丢失。

4 如果不幸中招，服务端正在使用Long类型作为大整数的返回，有哪些办法解决？

需要分情况。

1）通过Web的ajax异步接口，以Json串的形式返回给前端

方案一：如果，返回Long型所在的POJO对象在其他地方无使用，那么可以将后端的Long型直接修改成String型。

方案二：如果，返回给前端的Json串是将一个POJO对象Json序列化而来，并且这个POJO对象还在其他地方使用，而无法直接将其中的Long型属性直接改为String，那么可以采用以下方式：

String orderDetailString = JSON.toJSONString(orderVO, SerializerFeature.BrowserCompatible);

SerializerFeature.BrowserCompatible 可以自动将数值变成字符串返回，解决精度问题。

方案三：如果，上述两种方式都不适合，那么这种方式就需要后端返回一个新的String类型，前端使用新的，并后续上线后下掉老的Long型（推荐使用该方式，因为可以明确使用String型，防止后续误用Long型）。

2）使用node的方式，直接通过调用后端接口的方式获取

方案一：使用npm的js-2-java的 java.Long(orderId) 方法兼容一下。

方案二：后端接口返回一个新的String类型的订单ID，前端使用新的属性字段（推荐使用，防止后续踩坑）。