快速入门数据结构和算法

一 前言

1 为什么要学习算法和数据结构？

• 解决特定问题。
• 深度优化程序性能的基础。
• 学习一种思想：如何把现实问题转化为计算机语言表示。

2 业务开发要掌握到程度？

• 了解常见数据结构和算法，沟通没有障碍。
• 活学活用：遇到问题时知道要用什么数据结构和算法去优化。

二 数据结构基础

1 什么是数据结构？

数据结构是数据的组织、管理和存储格式，其使用目的是为了高效的访问和修改数据。

数据结构是算法的基石。如果把算法比喻成美丽灵动的舞者，那么数据结构就是舞者脚下广阔而坚实的舞台。

2 物理结构和逻辑结构的区别？

物理结构就像人的血肉和骨骼，看得见，摸得着，实实在在，如数组、链表。

逻辑结构就像人的思想和精神，它们看不见、摸不着，如队列、栈、树、图。

3 线性存储结构和非线性存储结构的区别？

• 线性：元素之间的关系是一对一的，如栈、队列。


• 非线性：每个元素可能连接0或多个元素，如树、图。

三 算法基础

1 什么是算法？

• 数学：算法是用于解决某一类问题的公式和思想。


• 计算机：一系列程序指令，用于解决特定的运算和逻辑问题。

2 如何衡量算法好坏？

• 时间复杂度：运行时间长短。
• 空间复杂度：占用内存大小。

3 怎么计算时间复杂度？

大O表示法（渐进时间复杂度）：把程序的相对执行时间函数T(n)简化为一个数量级，这个数量级可以是n、n^2、logN等。

推导时间复杂度的几个原则：

• 如果运行时间是常数量级，则用常数1表示。
• 只保留时间函数中的最高阶项。
• 如果最高阶项存在，则省去最高项前面的系数。

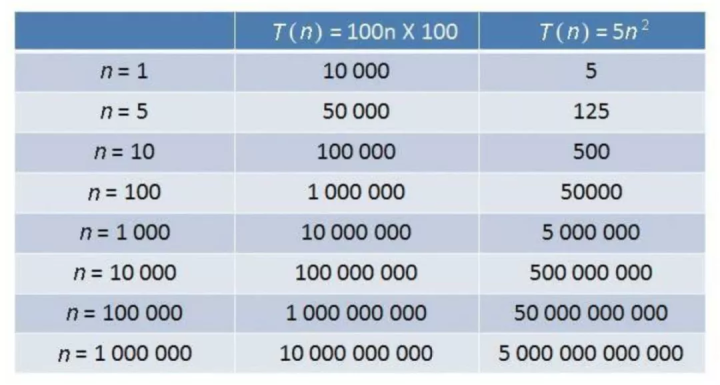
时间复杂度对比：O(1) > O(logn) > O(n) > O(nlogn) > O(n^2)。

不同时间复杂度算法运行次数对比：

4 怎么计算空间复杂度？

常量空间 O(1)：存储空间大小固定，和输入规模没有直接的关系。

线性空间 O(n)：分配的空间是一个线性的集合，并且集合大小和输入规模n成正比。

二维空间 O(n^2)：分配的空间是一个二维数组集合，并且集合的长度和宽度都与输入规模n成正比。

递归空间 O(logn)：递归是一个比较特殊的场景。虽然递归代码中并没有显式的声明变量或集合，但是计算机在执行程序时，会专门分配一块内存空间，用来存储“方法调用栈”。执行递归操作所需要的内存空间和递归的深度成正比。

5 如何定义算法稳定性？

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

6 有哪些常见算法？

首先要明确：特定算法解决特定问题。

• 字符串：暴力匹配、BM、KMP、Trie等。
• 查找：二分查找、遍历查找等。
• 排序：冒泡排序、快排、计数排序、堆排序等。
• 搜索：TFIDF、PageRank等。
• 聚类分析：期望最大化、k-meanings、k-数位等。
• 深度学习：深度信念网络、深度卷积神经网络、生成式对抗等。
• 异常检测：k最近邻、局部异常因子等。
• ......

其中，字符串、查找、排序算法是最基础的算法。

四 常见数据结构

1 数组

1）什么是数组？

数据是有限个相同类型的变量所组成的有序集合。数组中的每一个变量被称为元素。

2）数组的基本操作？

读取O(1)、更新O(1)、插入O(n)、删除O(n)、扩容O(n)。

2 链表

1）什么是链表？

链表是一种在物理上非连续、非顺序的数据结构，由若干个节点组成。

单向链表的每一个节点又包含两部分，一部分是存放数据的变量data，另一部分是指向下一个节点的指针next。

2）链表的基本操作？

读取O(n)、更新O(1)、插入O(1)、删除O(1)。

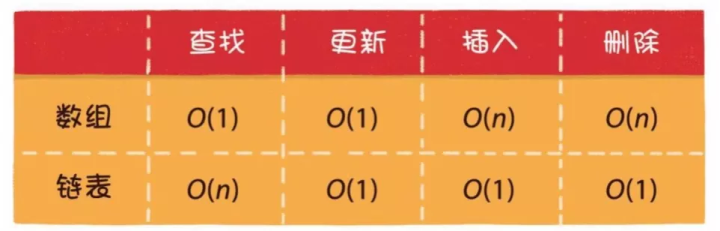
3）链表 VS 数组

数组：适合多读、插入删除少的场景。

链表：适用于插入删除多、读少的场景。

3 栈

1）什么是栈？

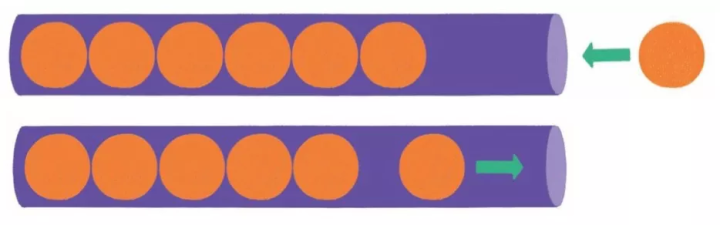
栈是一种线性逻辑数据结构，栈的元素只能后进先出。最早进入的元素存放的位置叫做栈底，最后进入的元素存放的位置叫栈顶。

一个比喻，栈是一个一端封闭一端的开放的中空管子，队列是两端开放的中空管子。

2）如何实现栈？

数组实现：

链表实现：

3）栈的基本操作

入栈O(1)、出栈O(1)。

4）栈的应用？

• 回溯历史，比如方法调用栈。
• 页面面包屑导航。

4 队列

1）什么是队列？

一种线性逻辑数据结构，队列的元素只能后进后出。队列的出口端叫做队头，队列的入口端叫做队尾。

2）如何实现队列？

数组实现：

链表实现：

3）队列的基本操作？

入队 O(1)、出队 O(1)。

4）队列的应用

• 消息队列
• 多线程的等待队列
• 网络爬虫的待爬URL队列

5 哈希表

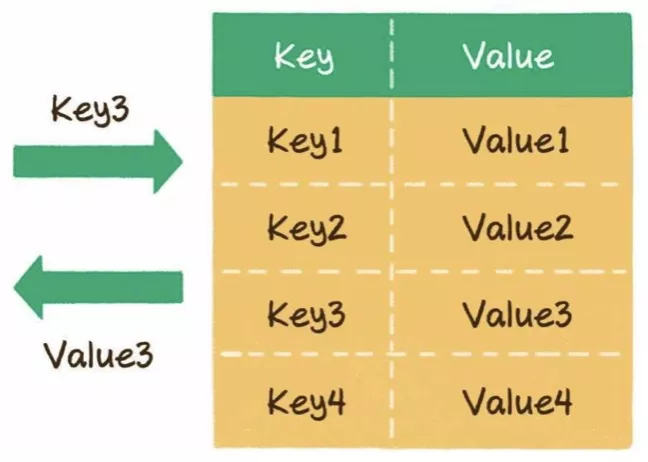
1）什么是哈希表？

一种逻辑数据结构，提供了键（key）和值（value）的映射关系。

2）哈希表的基本操作？

写入：O(1)、读取：O(1)、扩容O(n)。

3）什么是哈希函数？

哈希表本质上是一个数组，只是数组只能根据下标，像a[0] a[1] a[2] a[3] 这样来访问，而哈希表的key则是以字符串类型为主的。

通过哈希函数，我们可以把字符串或其他类型的key，转化成数组的下标index。

如给出一个长度为8的数组，则：

当key=001121时，

index = HashCode ("001121") % Array.length = 7

当key=this时，

index = HashCode ("this") % Array.length = 6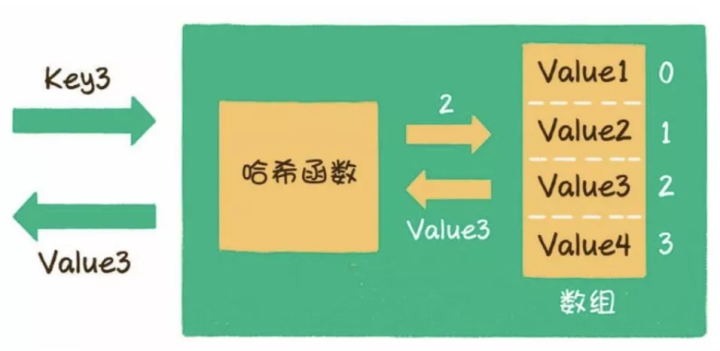

4）什么是哈希冲突？

不同的key通过哈希函数获得的下标有可能是相同的，例如002936这个key对应的数组下标是2，002947对应的数组下标也是2，这种情况就是哈希冲突。

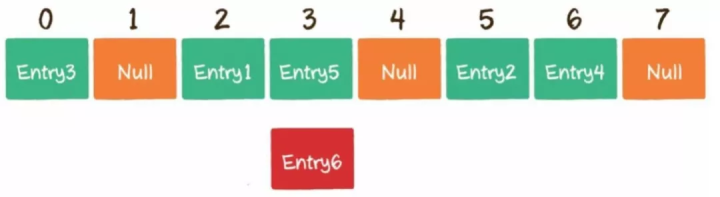
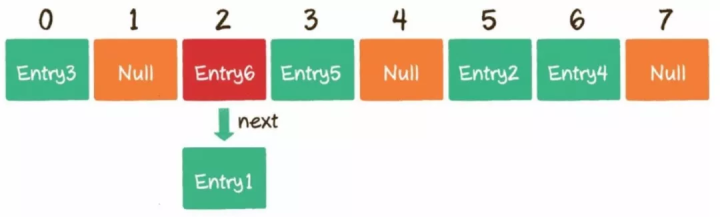
5）如何解决哈希冲突？

开放寻址法：例子Threadlocal。

链表法：例子Hashmap。

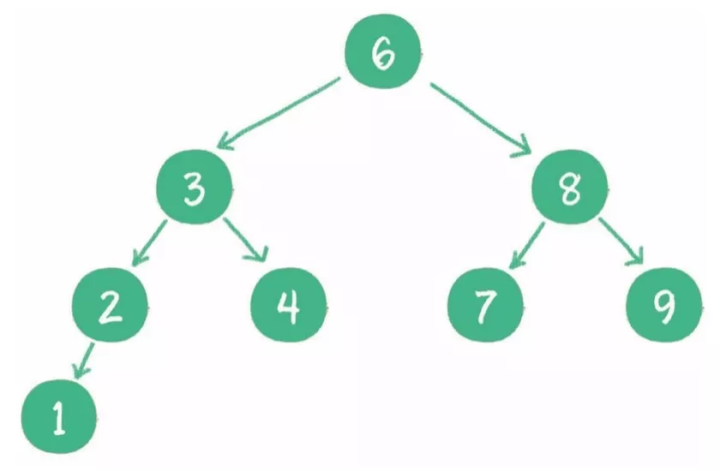
6 树

1）什么是树？

树（tree）是n（n≥0）个节点的有限集。

当n=0时，称为空树。在任意一个非空树中，有如下特点：

• 有且仅有一个特定的称为根的节点。


• 当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树。

2）树的遍历？

（1）深度优先

前序：根节点、左子树、右子树。

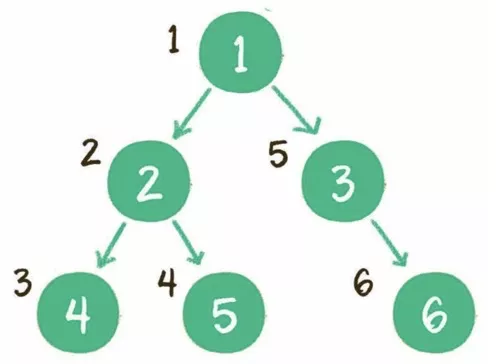
中序：左子树、根节点、右子树。

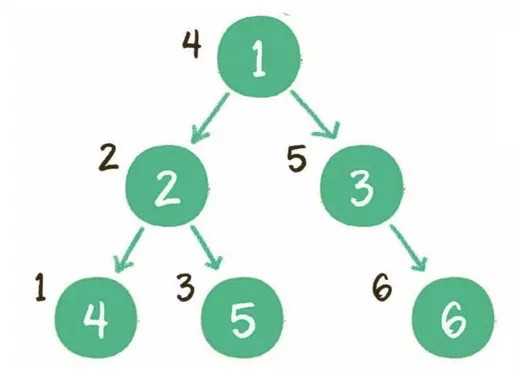
后序：左子树、右子树、根节点。

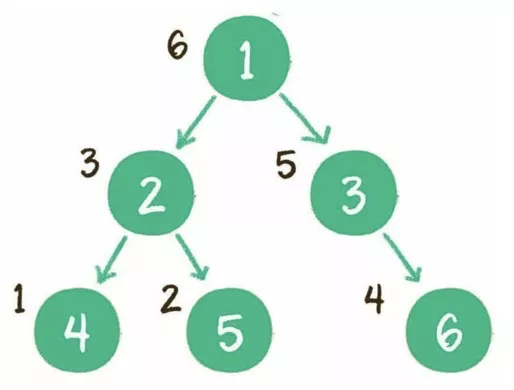
实现方式：递归或栈。

（2）广度优先

层序：一层一层遍历。

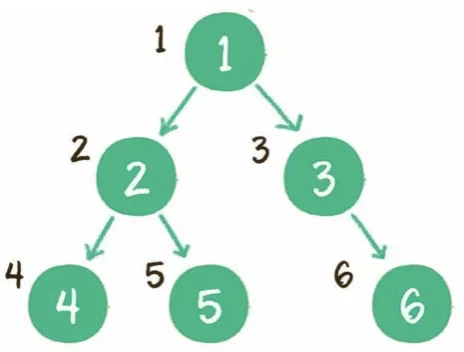
实现方式：队列。

7 二叉树

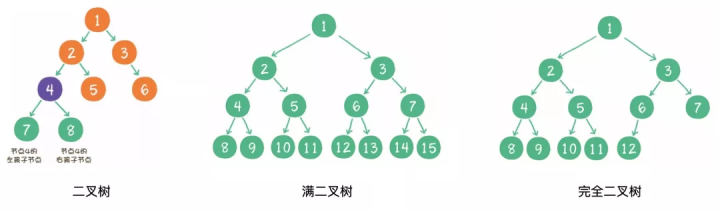
1）什么是二叉树?

二叉树（binary tree）是树的一种特殊形式。二叉，顾名思义，这种树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩子节点。

2）什么是满二叉树?

一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

3）什么是完全二叉树?

对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

8 二叉查找树

1）什么是二叉查找树？

二叉查找树在二叉树的基础上增加了以下几个条件：

• 如果左子树不为空，则左子树上所有节点的值均小于根节点的值。


• 如果右子树不为空，则右子树上所有节点的值均大于根节点的值。

• 左、右子树也都是二叉查找树。

2）二叉查找树的作用？

• 查找==》二分查找。
• 排序==》中序遍历。

3）二叉树的实现方式？

• 链表。
• 数组：对于稀疏二叉树来说，数组表示法是非常浪费空间的。

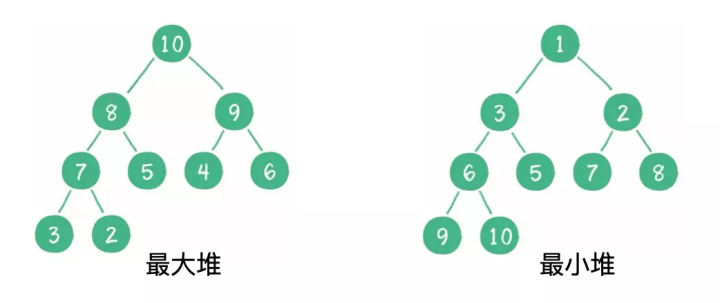
9 二叉堆

1）什么是二叉堆？

二叉堆是一种特殊的完全二叉树，它分为两个类型：最大堆和最小堆。

• 最大堆的任何一个父节点的值，都大于或等于它左、右孩子节点的值。


• 最小堆的任何一个父节点的值，都小于或等于它左、右孩子节点的值。

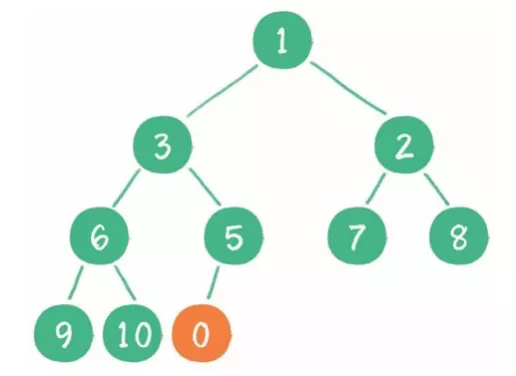
2）二叉堆的基本操作？

（1）插入：插入最末，节点上浮。

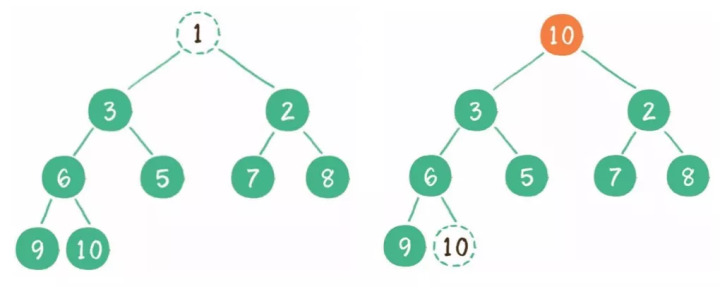
（2）删除：删除头节点，尾节点放到头部，再下沉。

（3）构建二叉堆：二叉树==》二叉堆，所有非叶子节点依次下沉。

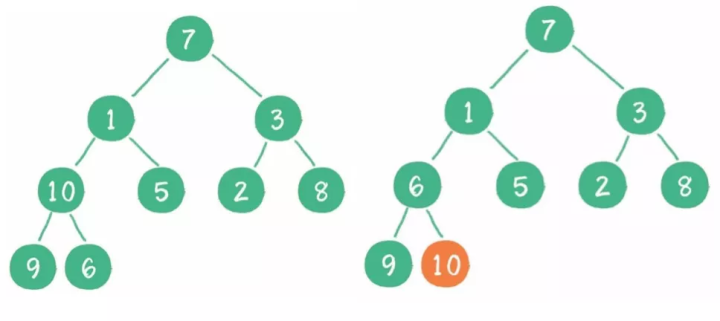
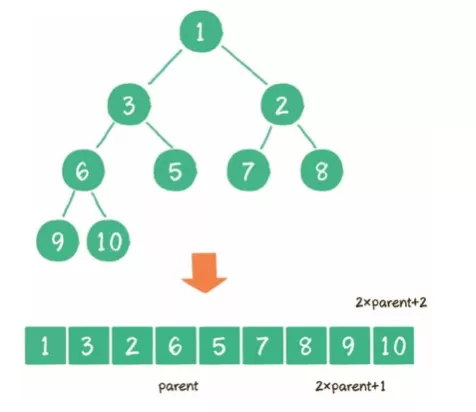
3）二叉堆的实现方式？

数组：

五 常见排序算法

1 十大经典排序算法

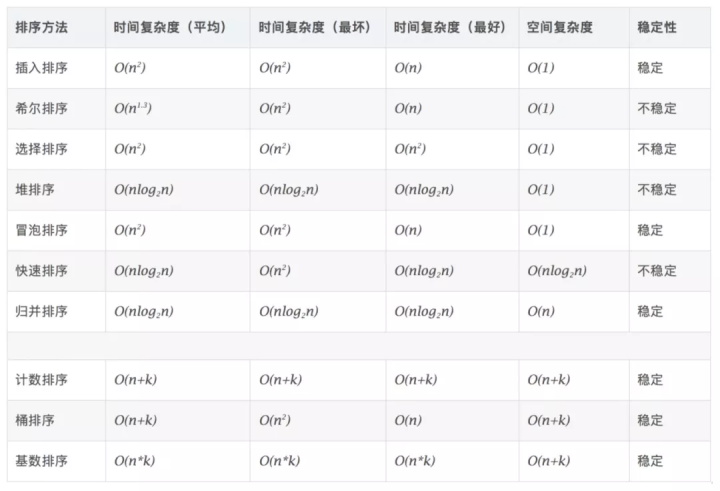
2 冒泡排序

1）算法描述

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

2）实现步骤

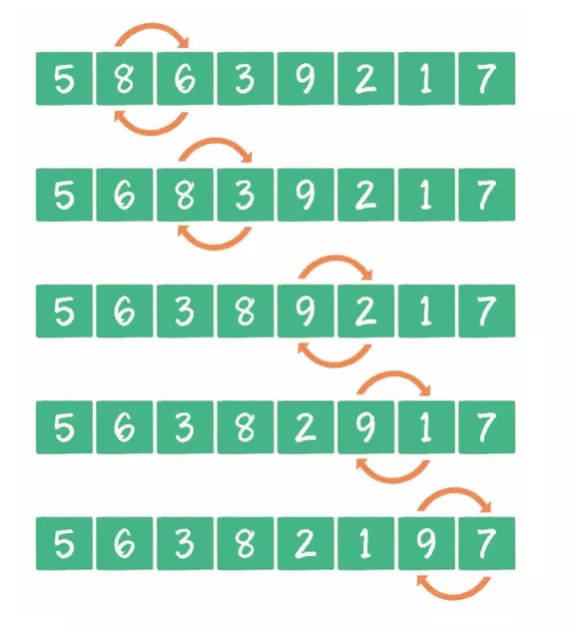
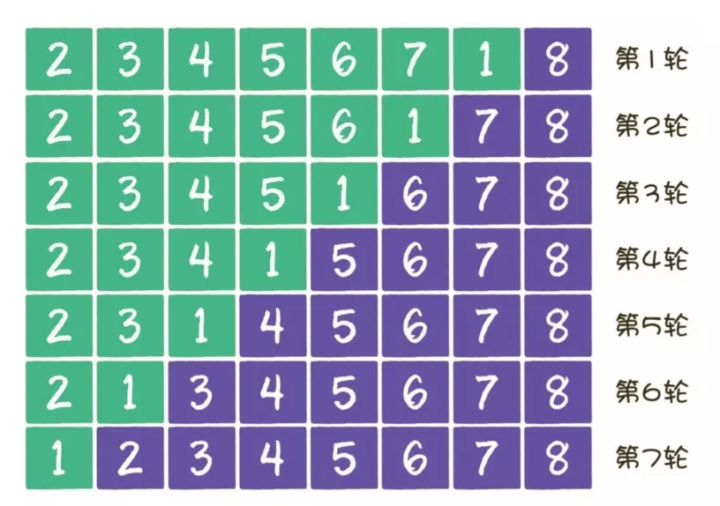
• 比较相邻的元素。如果第一个比第二个大，就交换它们两个。


• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数。

• 针对所有的元素重复以上的步骤，除了最后一个。


• 重复步骤1~3，直到排序完成。

3）优缺点

• 优点：实现和理解简单。


• 缺点：时间复杂度是O(n^2)，排序元素多时效率比较低。

4）适用范围

数据已经基本有序，且数据量较小的场景。

5）场景优化

（1）已经有序了还再继续冒泡问题

• 本轮排序中，元素没有交换，则isSorted为true，直接跳出大循环，避免后续无意义的重复。

（2）部分已经有序了，下一轮的时候但还是会被遍历

• 记录有序和无序数据的边界，有序的部分在下一轮就不用遍历了。

（3）只有一个元素不对，但需要走完全部轮排序

• 鸡尾酒排序：元素的比较和交换是双向的，就像摇晃鸡尾酒一样。

3 归并排序

1）算法描述

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。递归的把当前序列分割成两半（分割），在保持元素顺序的同时将上一步得到的子序列集成到一起（归并），最终形成一个有序数列。

2）实现步骤

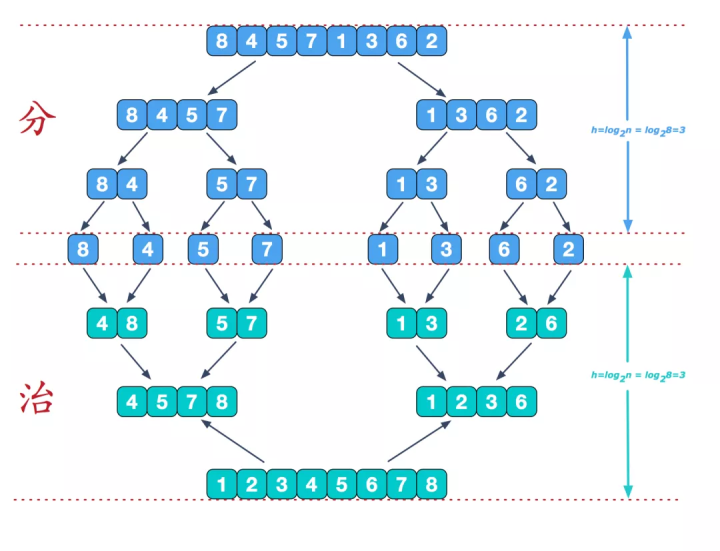
图源：https://www.cnblogs.com/chengxiao/p/6194356.html

• 把长度为n的输入序列分成两个长度为n/2的子序列。


• 对这两个子序列分别采用归并排序。

• 将两个排序好的子序列合并成一个最终的排序序列。

3）优缺点

优点：

• 性能好且稳定，时间复杂度为O(nlogn) 。
• 稳定排序，适用场景更多。

缺点：

• 非原地排序，空间复杂度高。

4）适用范围

大数据量且期望要求排序稳定的场景。

4 快速排序

1）算法描述

快速排序使用分治法策略来把一个序列分为较小和较大的2个子序列，然后递归地排序两个子序列，以达到整个数列最终有序。

2）实现步骤

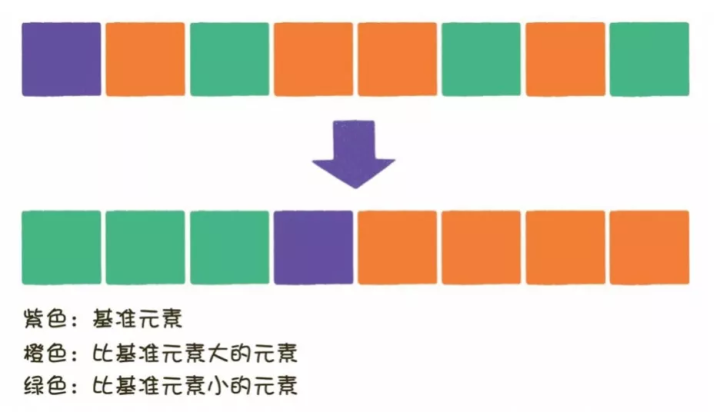
• 从数列中挑出一个元素，称为 “基准值”（pivot）。


• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

• 递归地对【小于基准值元素的子数列】和【大于基准值元素的子数列】进行排序。

3）优缺点

优点：

• 性能较好，时间复杂度最好为O(nlogn)，大多数场景性能都接近最优。
• 原地排序，时间复杂度优于归并排序。

缺点：

• 部分场景，排序性能最差为O(n^2)。
• 不稳定排序。

4）适用范围

大数据量且不要求排序稳定的场景。

5）场景优化

（1）每次的基准元素都选中最大或最小元素

• 随机选择基准元素，而不是选择第一个元素。
• 三数取中法，随机选择三个数，取中间数为基准元素。

（2）数列含有大量重复数据

• 大于、小于、等于基准值。

（3）快排的性能优化

• 双轴快排：2个基准数，例子：Arrays.sort() 。

5 堆排序

1）算法描述

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

2）实现步骤

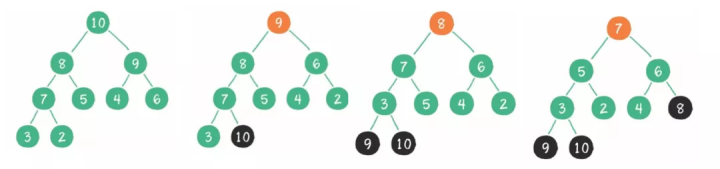
• 将初始待排序关键字序列(R1,R2….Rn)构建成最大堆，此堆为初始的无序区。


• 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]。

• 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

3）优缺点

优点：