最短路径算法解析

现在，我们准备介绍计算机科学史上伟大的成就之一：Dijkstra最短路径算法。这个算法适用于边的长度均不为负数的有向图，它计算从一个起始顶点到其他所有顶点的最短路径的长度。在正式定义这个问题（3.1节）之后，我们讲解这个算法（3.2节）以及它的正确性证明（3.3节），然后介绍一个简单直接的实现（3.4节）。在第4章中，我们将看到这种算法的一种令人惊叹的快速实现，它充分利用了堆这种数据结构。

3.1　单源最短路径问题

3.1.1　问题定义

Dijkstra算法解决了单源最短路径问题。[2]

问题：单源最短路径
输入：有向图G=(V, E)，起始顶点s∈V，并且每条边e∈E的长度e均为非负值。
输出：每个顶点v∈V的dist(s,v)。

注意，dist(s,v)这种记法表示从s到v的最短路径的长度（如果不存在从s到v的路径，dist(s,v)就是+∞）。所谓路径的长度，就是组成这条路径的各条边的长度之和。例如，在一个每条边的长度均为1的图中，路径的长度就是它所包含的边的数量。从顶点v到顶点w的最短路径就是所有从v到w的路径中长度最短的。

例如，如果一个图表示道路网，每条边的长度表示从一端到另一端的预期行车时间，那么单源最短路径问题就成为计算从一个起始顶点到所有可能的目的地的行车时间的问题。

小测验3.1
考虑单源最短路径问题的下面这个输入，起始顶点为s，每个边都有一个标签标识了它的长度：
从s出发到s、v、w和t的最短距离分别是多少？
（a）0，1，2，3
（b）0，1，3，6
（c）0，1，4，6
（d）0，1，4，7
（正确答案和详细解释参见3.1.4节。）

3.1.2　一些前提条件

方便起见，我们假设本章中的输入图是有向图。经过一些微小的戏剧性修改之后，Dijkstra算法同样适用于无向图（可以进行验证）。

另一个前提条件比较重要。问题陈述已经清楚地表明：我们假设每条边的长度是非负的。在许多应用中（例如计算行车路线），边的长度天然就是非负的（除非涉及时光机器），完全不需要担心这个问题。但是，我们要记住，图的路径也可以表示抽象的决策序列。例如，也许我们希望计算涉及购买和销售的金融交易序列的利润。这个问题相当于在一个边的长度可能为正也可能为负的图中寻找最短路径。在边的长度可能为负的应用中，我们不应该使用Dijkstra算法，具体原因可以参考3.3.1节。[3]

3.1.3　为什么不使用宽度优先的搜索

如2.2节所述，宽度优先的搜索的一个“杀手”级应用就是计算从一个起始顶点出发的最短路径。我们为什么需要另一种最短路径算法呢？

记住，宽度优先的搜索计算的是从起始顶点到每个其他顶点的边数最少的路径，这是单源最短路径问题中每条边的长度均为1这种特殊情况。我们在小测验3.1中看到，对于通用的非负长度边，最短路径并不一定是边数最少的路径。最短路径的许多应用，例如计算行车路线或金融交易序列，不可避免地涉及不同长度的边。

但是，读者可能会觉得，通用的最短路径问题与这种特殊情况真的存在这么大的区别吗？如图3.1所示，我们不能把一条更长的边看成3条长度为1的边组成的路径吗？

图3.1　路径

事实上，“一条长度为正整数

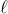
的边”和“一条由

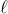
条长度为1的边所组成的路径”之间并没有本质的区别。在原则上，我们可以把每条边展开为由多条长度为1的边组成的路径，然后应用宽度优先的搜索对图进行展开来解决单源最短路径问题。

这是把一个问题简化为另一个问题的一个例子。在这个例子中，就是从边的长度为正整数的单源最短路径问题简化为每条边的长度均为1的特殊情况。

这种简化所存在的主要问题是它扩大了图的规模。如果所有边的长度都是小整数，那么这种扩张并不是严重的问题。但在实际应用中，情况并不一定如此。某条边的长度很可能比原图中顶点和边的总数还要大很多！宽度优先的搜索在扩张后的图中的运行效率是线性时间，但这种线性时间并不一定接近原图长度的线性时间。

Dijkstra算法可以看成是在扩张后的图上执行宽度优先的搜索的一种灵活模拟，它只对原始输入图进行操作，其运行时间为近似线性。

关于简化
如果一种能够解决问题B的算法可以方便地经过转换解决问题A，那么问题A就可以简化为问题B。例如，计算数组的中位元素的问题可以简化为对数组进行排序的问题。简化是算法及其限制的研究中非常重要的概念，具有极强的实用性。
我们总是应该寻求问题的简化。当我们遇到一个似乎是新的问题时，总是要问自己：这个问题是不是一个我们已经知道怎样解决的问题的伪装版本呢？或者，我们是不是可以把这个问题的通用版本简化为一种特殊情况呢？

3.1.4　小测验3.1的答案

正确答案：（b）。从s到本身的最短路径的长度为0以及从s到v的最短路径的长度为1不需要讨论。顶点w稍微有趣一点。从s到w的其中一条路径是有向边(s,w)，它的长度是4。但是，通过更多的边可以减少总长度：路径s→v→w的长度只有1+2=3，它是最短的s−w路径。类似地，从s到t的每条经过两次跳跃的路径的长度为7，而那条更迂回的路径的长度只有1+2+3=6。

3.2　Dijkstra算法

3.2.1　伪码

Dijkstra算法的高层结构与第2章的图搜索算法相似。[4]它的主循环的每次迭代处理一个新的顶点。这个算法的高级之处在于它采用了一种非常“聪明”的规则选择接下来处理哪个顶点：就是尚未处理的顶点中看上去最靠近起始顶点的那一个。下面的优雅伪码精确地描述了这个思路。

Dijkstra算法
输入：邻接列表表示形式的有向边G=(V,E)，对于每条边e∈E，它的长度都大于或等于0。
完成状态：对于每个顶点v，len(v)的值等于真正的最短路径长度dist(s,v)。
// 初始化 1 X := {s} 2 len(s) := 0, len(v) := +∞ for每个v≠s // 主循环 3 while 存在一条边(v,w)，v∈X,w∉X do 4 (v*, w*) := 具有最小的len(v)+ 的边 5 把w*加到X中 6 len(w*):= len(v*)+

集合X包含了这个算法已经处理过的顶点。一开始，X只包含了起始顶点（当然，len(s)=0），然后这个集合不断增长，直到它覆盖了从s可以到达的所有顶点。当这个算法把一个顶点添加到X时，它同时为这个顶点的len值赋一个有限的值。主循环的每次迭代向X添加一个新顶点，即某条从X跨越到V−X的边(v,w)的头顶点（图3.2）。（如果不存在这样的边，算法就会终止，对于所有的

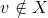
，都有len(v)=+∞。）符合条件的边可能有多条，Dijkstra算法选择Dijkstra得分最低的那条边(v*,w*)，它被定义为

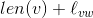
（3.1）

注意，Dijkstra得分是根据边进行定义的，顶点w∉X可能是许多不同的从X跨越到V−X的边的头顶点，这些边一般具有不同的Dijkstra得分。

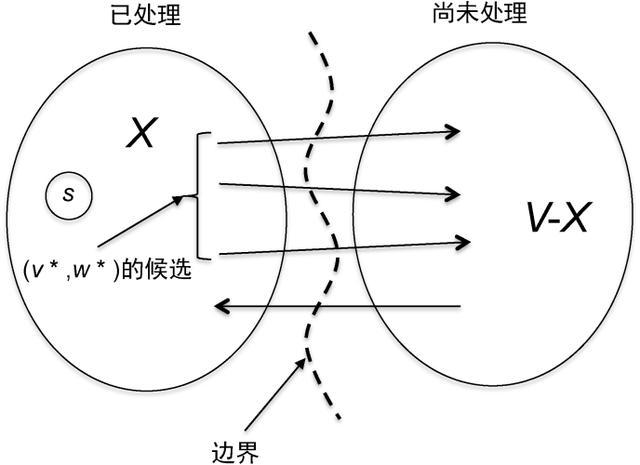
图3.2　Dijkstra算法的每次迭代处理一个新顶点，即一条从X跨越到V−X的边的头顶点

我们可以把一条边(v,w)（v∈X,w∉X）的Dijkstra得分与一个假想相关联。这个假想就是：从s到w的最短路径是由一条从s到v的最短路径（其长度应该是len(v)）和一条紧随其后的边(v,w)（其长度为

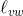
）所组成的。因此，Dijkstra算法根据已经计算的最短路径的长度，并根据从X跨越到V−X的各条边的长度，在尚未处理的顶点中选择添加看上去最靠近s的那个顶点。在把w*添加到X时，这个算法把len(w*)作为从s出发的假想最短路径的长度，也就是边(v*,w*)的Dijkstra得分len(v*)+

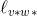
。后面的定理3.1规范描述的Dijkstra算法的神奇之处就在于这个假想保证是正确的，即使这个算法目前只是观察了整个图的很小一部分。[5]

3.2.2　一个例子

让我们根据小测验3.1的例子对Dijkstra算法进行试验：

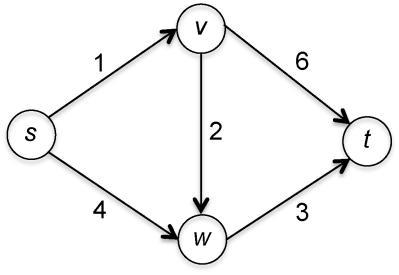
一开始，集合X只包含了顶点s，且len(s)=0。在主循环的第1次迭代中，有(s,v)和(s,w)两条边从X跨越到V−X（因此它们均可以扮演(v*,w*)的角色）。这两条边的Dijkstra得分（由式（3.1）所定义）分别是len(s)+

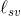
= 0+1=1和len(s)+

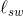
=0+4=4。由于前者的得分更低，因此它的头顶点v就被添加到X中，并且len(v)被赋值为边(s,v)的Dijkstra得分，其值为1。在第2次迭代时，X={s,v}，有(s,w)、(v,w)和(v,t)共3条边可以扮演(v*,w*)的角色。它们的Dijkstra得分分别是0+4=4、1+2=3和1+6=7。由于(v,w)具有最低的Dijkstra得分，因此w被添加到X中，len(w)被赋值为3（(v,w)的Dijkstra得分）。我们已经知道哪个顶点会在最后一次迭代中被添加到X（唯一未被处理的顶点t），但仍然需要确定它是因为哪条边而被添加（为了计算len(t)）。由于(v,t)和(w,t)的Dijkstra得分分别是1+6=7和3+3=6，因此len(t)被设置为较小的值6。现在，集合X包含了所有的顶点，不再有任何边从X跨越到V−X，因此算法就宣告结束。len(s)=0，len(v)=1，len(w)=3，len(t)=6这几个值与我们在小测验3.1中所验证的真正最短路径的长度是匹配的。

当然，一个算法在一个特定的例子上是正确的并不能就此说明它在所有情况下都是正确的！[6]事实上，Dijkstra算法并不能正确地计算边的长度可能为负时的最短路径长度（如3.3.1节所述）。我们在一开始就应该对Dijkstra算法保持怀疑，要求给出它的证明，至少要证明对于边的长度非负的图，它能够正确地解决单源最短路径问题。

*3.3　为什么Dijkstra算法是正确的

3.3.1　一种虚假的简化

读者可能会觉得奇怪，边的长度是否为负为什么会有影响呢？难道不能把每条边的长度都加上同一个很大的数字，让所有边的长度都为非负吗？

这是一个很好的问题，我们总是应该寻求是否能够把待解决的问题简化为已经知道怎样解决的问题。可惜的是，我们不能按照这种方式把通用边长的单源最短路径问题简化为非负边长的特殊情况。问题在于从一个顶点到另一个顶点的不同路径并不一定具有相同数量的边。如果我们把每条边的长度都加上一个数，不同路径所增加的数量可能并不相同，新图的最短路径可能与原图并不相同。图3.3所示的是一个简单的例子。

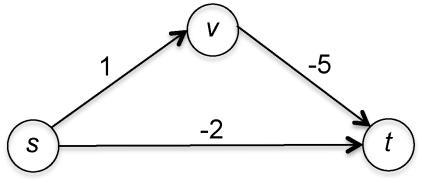
图3.3　单源最短路径问题举例

从s到t共有两条路径：直接路径（长度为-2）和经过两次跳跃的路径s→v→t（长度为1+(-5)=4）。

后者的长度更长（即绝对值更大的负值），因此是最短的s-t路径。

为了使这张图具有非负的边长，我们可以把每条边的长度都加上5，结果如图3.4所示。

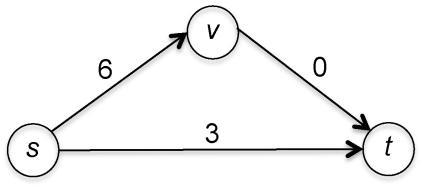
图3.4　每条边长度加5后的路径

从s到t的最短路径发生了变化，现在是直达的s−t边（长度为3，小于另一条长度为6的路径）。在转换后的图中运行最短路径算法所产生的结果与原图不同。

3.3.2　Dijkstra算法的一个糟糕例子

如果我们在一个某些边的长度为负的图（例如3.3.1节中的图）上运行Dijkstra算法，那么会发生什么情况呢？一开始，X={s}且len(s)=0，此时一切正常。但是，在主循环的第1次迭代中，这个算法计算边(s,v)和(s,t)的Dijkstra得分，其值分别是len(s)+

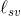
= 0+1=1和len(s)+

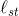
=0+(−2) = −2。后者的得分更低，因此这个算法把顶点t添加到X中，并把len(t)赋值为−2。我们已经注意到，从s到t的实际最短路径（路径s→v→t）的长度是−4。因此，我们可以得出结论，如果图中某些边的长度为负，Dijkstra就无法计算正确的最短路径长度。

3.3.3　非负边长时的正确性

算法的正确性证明多少带有一点学究气。对于学生们在直觉上强烈地认为是正确的算法，我常常会略过它们的正确性证明。Dijkstra算法并不是这样。首先，它不适用于边的长度为负的图（即使是非常简单的图，如3.3.1节所述）的情况已经让我们心生疑虑。其次，Dijkstra得分这个概念（见3.1节）看上去有点神秘甚至有点随意，它为什么非常重要呢？由于这些疑虑，并且由于它是一种非常重要的基本算法，因此我们需要花点时间仔细地证明它的正确性（在边的长度非负的图中）。

定理3.1（Dijkstra算法的正确性）　对于每个有向图G = (V, E)、每个起始顶点s并且所有边长均为非负值，对于每个顶点v∈V，Dijkstra算法的结论len(v) = dist(s,v)都成立。

归纳之旅

我们的计划是根据主循环的迭代数量进行归纳，逐个计算Dijkstra算法的最短路径长度的正确性。记住，根据数学归纳法所进行的证明采用了一个相对刻板的模板，它的目的是建立一个对于每个正整数k都成立的断言P(k)。在定理3.1的证明中，我们把P(k)定义为：“在Dijkstra算法中，对于第k个添加到X中的顶点v，存在len(v)=dist(s,v)。”

与递归算法类似，通过数学归纳法所进行的证明分为一个基本条件和一个归纳步骤两个部分。基本条件直接证明了P(1)是正确的。在归纳步骤中，我们假设P(1),…,P(k-1)都是正确的，这称为归纳假设。我们使用这个假设证明P(k)也是正确的。如果基本条件和归纳步骤得到了证明，那么P(k)对于每个正整数k肯定也是正确的。根据基本条件，P(1)是正确的。不断地应用归纳步骤显示了对于任意大的k值，P(k)都是正确的。

关于证明的阅读
数学论证根据前提条件推导出结论。在阅读证明的时候，总是要保证理解了论证中的每个前提条件的用法，并理解为什么缺少任何一个前提条件就会导致论证失败。
记住这一点之后，仔细观察定理3.1的证明中两个关键的前提条件所扮演的角色：边的长度是非负的以及算法总是会选择具有最低Dijkstra得分的边。在证明定理3.1时，如果不能支持这两个前提条件，那么证明过程必然是失败的。

定理3.1的证明

我们继续进行归纳，P(k)表示Dijkstra算法可以正确地计算添加到集合X的第k个顶点的最短路径的长度。对于基本条件（k =1），我们知道添加到X的第1个顶点是起始顶点s。Dijkstra算法把0赋值给len(s)。由于每条边都具有非负的长度，因此从s到它本身的最短路径是一条空路径，长度为0。因此，len(s)=0=dist(s,s)，这就证明了P(1)是成立的。

对于归纳步骤，选择k >1并假设P(1),…,P(k−1)都是正确的，对于Dijkstra算法添加到X的前k−1个顶点，len(v)=dist(s,v)。设w*表示添加到X的第k个顶点，并用(v*,w*)表示在对应的那次迭代中（此时v*必然已经在X中）所选择的边。算法把len(w*)赋值为这条边的Dijkstra得分，即len(v*)+

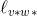
。我们希望这个值与真正的最短路径长度dist(s,w*)相同，但事实确实如此吗？

我们分两个部分论证这个结论的正确性。首先，我们证明真正的长度dist(s,w*)只可能小于算法所推测的len(w*)，即dist(s,w*)≤len(w*)。由于当边(v*,w*)被选中时，v*已经在X中，因此它是添加到X的前k−1个顶点之一。根据归纳假设，Dijkstra算法正确地计算了v*的最短路径长度：len(v*)=dist(s,v*)。

具体地说，存在一条从s到v*的路径P，它的长度正好是len(v*)。在P的末端添加边(v*,w*)就产生了一条从s到w*的路径P*，它的长度是len(v*)+

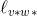
=len(w*)（图3.5）。s−w*路径的最短路径除了候选路径P*之外不会再有其他路径，因此dist(s,w*)不可能大于len(w*)。

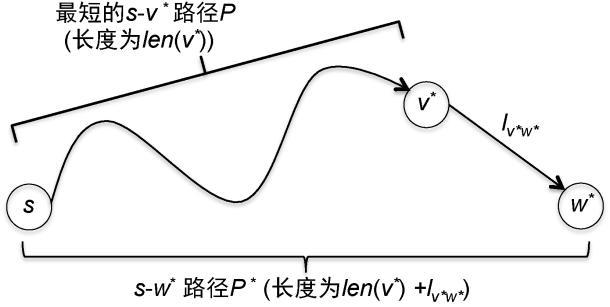
图3.5　在s−v*最短路径的末尾添加边(v*, w*)，产生一条s到w*的最短路径P*，其长度为len(v*)+

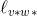
现在，我们讨论反方向的不等式dist(s,w*)≥len(w*)（证明这一点之后就可以满足len(w*)=dist(s,w*)）。换而言之，我们希望证明图3.2中的路径P*确实是s−w*的最短路径，每条与之竞争的s−w*路径的长度都不会小于len(w*)。

我们随意选择一条s−w*的竞争路径P'。我们对P'所知甚少。但是，我们知道它源于s，终于w*。在迭代之初，s属于集合X但w*不属于X。由于它是从X中开始并在X之外结束，因此路径P'跨越了X和V−X的边界1次（图3.6）。设(y, z)表示跨越边界的P'的第1条边（y∈X且z∉X）。[7]

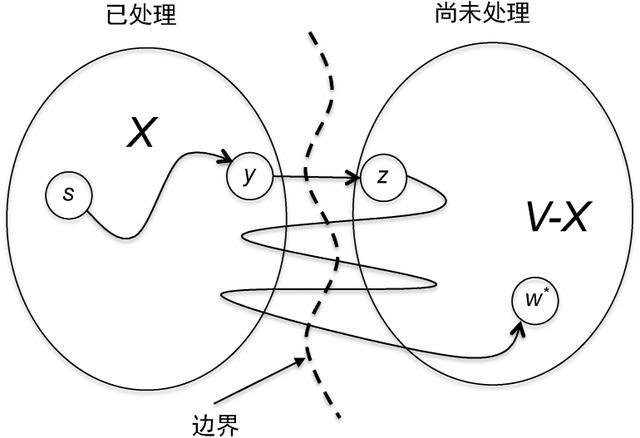
图3.6　每条s−w*路径从X跨越到V−X至少1次

为了论证P'的长度不会小于len(w*)，我们独立地考虑它的3个片段：P'从s到y的起始部分、边(y, z)以及从z到w*的最终部分。起始部分不可能短于从s到y的最短路径，因此它的长度至少是dist(s, y)。边(y, z)的长度是

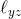
。我们对路径的最终部分并不十分了解，它掩藏在算法尚未观察的顶点之中。但是，我们知道所有边的长度都是非负的！也就是说，它的总长度至少是0，如图3.7所示。

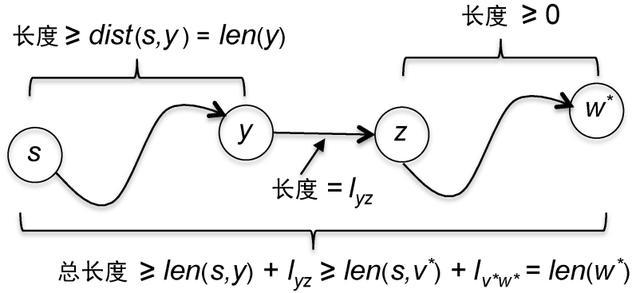
图3.7　总长度计算

把这3个部分的长度下界相加，可以得出：

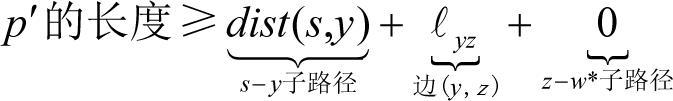
（3.2）

最后一个任务是把式（3.2）中的长度下界与指导算法决策的Dijkstra得分进行关联。由于y∈X，因此它是前k−1个添加到X的顶点之一，归纳假设表明了该算法会正确地计算它的最终路径长度：dist(s, y)=len(y)。因此，不等式（3.2）可以转换为

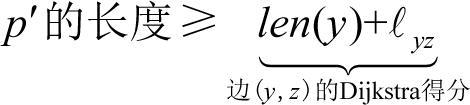
（3.3）